vae.py

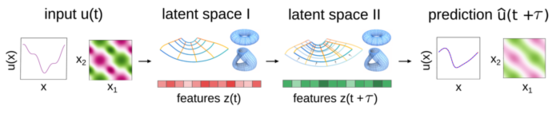
Variational Autoencoders (VAEs) for training neural networks and other models for learning latent structures from datasets based on Bayesian inference and variational approximations.

If you find these codes or methods helpful for your project, please cite our related work.

vae.eval_tilde_L_B(theta, phi, X_batch, **extra_params)

Evaluates the VAE loss function based on ELBO and the introduced regularization terms.

Parameters:

• theta (model) – model data structure for encoder.

• phi (model) – model data structure for the decoder.

• X_batch (Tensor) – collection of training data with which to compare the model results.

• extra_params (dict) – additional parameters (see examples and codes).

Returns:

loss (Tensor) – loss evaluation for \(\mathcal{L}_B\) (see paper for details).

extra_params [members]

Property	Description
m1_mc	number of samples to use in MC estimators
batch_size	size of training batch
total_N_xi	total number of x_i’s
num_dim_x	number of dimensions for x
num_dim_z	number of dimensions for z
device	cpu, gpu, or other device to use
beta	Kullback-Leibler weight term as in \(\beta\)-VAEs

vae.get_statistic_ELBO(theta, phi, X_batch, **extra_params)

Returns the Evidence Lower Bound (ELBO) for models. The \(ELBO = -\mathcal{L}_B\).

vae.get_statistic_KL(theta, phi, X_batch, **extra_params)

Compute estimate of the Kullback-Leibler divergence \(D_KL(q(z|x) | p(z)) = E_q[log(q(z|x))] - E_q[log(p(z))]\)

vae.get_statistic_LL(theta, phi, X_batch, **extra_params)

We use importance sampling to estimate the Log Likelihood. Discussion in Burda, 2016, paper on importance weighted AE.

\(LL = \log\left(p(\mathbf{x})\right)\approx\log\left(\frac{1}{m}\sum_{j = 1}^m \frac{\tilde{p}_{\theta_e,\theta_d}(\mathbf{x},\mathbf{z}^{(j)})}{\mathfrak{q}_{\theta_e}(\mathbf{z}^{(j)} | \mathbf{x})}\right).\)

The samples are taken \(\mathbf{z}^{(j)} \sim \mathfrak{q}_{\theta_e}(\mathbf{z}^{(j)} | \mathbf{x})\). Here the joint-probability under the VAE model is given by \(\tilde{p}_{\theta_e,\theta_d}(\mathbf{x},\mathbf{z}) = \mathfrak{p}_{\theta_d}(\mathbf{x} | \mathbf{z}) \mathfrak{p}_{\theta_d}(\mathbf{z}).\)

Parameters:

• theta (dict) – decoder model

• phi (dict) – encoder model

• X_batch (Tensor) – input points. Tensor of shape = [num_x,num_dim_x].

• extra_params (dict) – extra parameters (see examples and codes).

Returns:

LL (double) – statistic LL.

vae.get_statistic_RE(theta, phi, X_batch, **extra_params)

Compute estimate of the reconstruction error term \(RE = E_q[log(p(x|z))] - E_q[log(p(z))]\)

vae.loss_VAE_neg_tilde_L_B(X_batch, theta, phi, **extra_params)

Evaluates the VAE loss function based on ELBO estimator of the negative log probabiliy of the data set X, loss = \(-\tilde{\mathcal{L}}_B\)

Parameters:

• X_batch (Tensor) – collection of training samples.

• theta (model) – model data structure for encoder.

• phi (model) – model data structure for the decoder.

• extra_params (dict) – additional parameters (see examples and codes).

Returns:

loss (Tensor) – loss evaluation for \(-\mathcal{L}_B\).

extra_params [members]

Property	Description
m1_mc	number of samples to use in MC estimators
batch_size	size of training batch
total_N_xi	total number of x_i’s
num_dim_x	number of dimensions for x
num_dim_z	number of dimensions for z
device	cpu, gpu, or other device to use
beta	Kullback-Leibler weight term as in \(\beta\)-VAEs