Paul J. Atzberger

Associate Professor
Department of Mathematics
Department of Mechanical Engineering
PhD Mathematics � Courant Institute � New York University � 2003

Awards and Support

NSF Career Award, 2010 - 2015.
Hellman Faculty Fellowship, 2009 - 2010.
W.M. Keck Foundation, 2011 - 2014.
Institute for Collaborative Biotechnologies, 2008 - 2011.
NSF-DMS-0635535, 2006 - 2009.
Founders� Day Award, NYU, 1998.

Research Interests

Stochastic analysis and computational methods for Stochastic Partial Differential Equations (SPDEs).
Applications in the natural sciences and engineering.

Specific application areas include:

fluctuating hydrodynamics
fluid-structure interaction
soft materials and complex fluids
molecular biology : motor proteins, microtubules, aptamers
microfluidic and nanofluidic devices.

My work can be classified broadly as:

Stochastic Analysis
Statistical Physics
Numerical Analysis
Scientific Computing.

For a more detailed discussion of my work see the publications section or the research summaries.

Positions Available

Graduate and Undergraduate Researchers (Now hiring in Atzberger Research Group).?

Events

KITP Workshop : Physical Principles of Multiscale Modeling, Analysis, and Simulation in Soft Condensed Matter, (April 2012 - June 2012) [more information].

Publications

Spectral Analysis Methods for the Robust Measurement of the Flexural Rigidity of Biopolymers, D. Valdman, P.J. Atzberger, D. Yu, and M. T. Valentine, (accepted Bio. Phys. J.), (2012). [preprint PDF] Δ [full paper DOI]
Influence of Target Concentration and Background Binding on In Vitro Selection of Affinity Reagents, J. Wang, J. F. Rudzinski, Q. H. Gonga, H.T. Soh, P.J. Atzberger (submitted 2012), [preprint PDF] Δ
Stochastic Eulerian Lagrangian Methods for Fluid Structure Interactions with Thermal Fluctuations, P.J. Atzberger, J. of Comp. Phys., 230, pp. 2821--2837, (2011). [preprint PDF] Δ [arXiv] [full paper DOI]
Stochastic Reduction Method for Biological Chemical Kinetics using Time-Scale Separation, C.D. Pahlajani, M. Khammash, P.J. Atzberger, J. of Theor. Bio. Vol. 272, Iss. 1, 7 March, Pages 96-112, (2011). [preprint PDF] Δ [full paper DOI]
Experimental Study of the Separation Behavior of Nanoparticles in Micro- and Nano-Channels, M. Napoli, P.J. Atzberger, S. Pennathur, J. Microfluidics and Nanofluidics, Volume 10, Issue 1, Page 69, (2011). [preprint PDF] Δ [full paper DOI]
Spatially Adaptive Stochastic Numerical Methods for Intrinsic Fluctuations in Reaction-Diffusion Systems, P.J. Atzberger, J. Comp. Phys., Vol. 229, Iss. 9, 1 May, pp. 3474-3501, (2010). [preprint PDF] Δ [full paper DOI]
Simulation of Complex Fluids and Soft Materials using Stochastic Eulerian Lagrangian Methods with Shear Boundary Conditions, P.J. Atzberger, (2010), (preprint). [preprint PDF] Δ
Spatially Adaptive Stochastic Multigrid Methods for Fluid-Structure Systems with Thermal Fluctuations, P. J. Atzberger, (preprint), (2010). [preprint PDF] Δ
Hybrid Elastic and Discrete-Particle Approach to Biomembrane Dynamics with Application to the Mobility of Curved Integral Membrane Proteins, , A. Naji, P.J. Atzberger and F.L.H. Brown, Phys. Rev. Lett. 102, 138102, (2009). [preprint PDF] [full paper DOI]
A Microfluidic Pumping Mechanism Driven by Non-equilibrium Osmotic Effects, P.J. Atzberger, S.A. Isaacson, and C.S. Peskin, Physica D: Nonlinear Phenomena, Vol. 238, Iss. 14, July, pp. 1168-1179, (2009),[preprint PDF] Δ [full paper DOI]
Micromagnetic Selection of Aptamers in Microfluidic Channels, X. Lou, J. Qian, X. Yi, L. Viel, A.E. Gerdon, E.T. Lagally, P.J. Atzberger, A.J. Heeger, and H.T. Soh, PNAS, Vol. 106 No. 9 pp. 2989-2994, (2009), [preprint PDF] Δ [full paper DOI]
Analysis of Selection Approaches for Aptamer Molecular Libraries, J. Rudzinski, T. Soh, P.J. Atzberger, Technical Report, (2009), [technical report PDF] Δ
On the Foundations of the Stochastic Immersed Boundary Method, P.R. Kramer, C.S. Peskin, and P.J. Atzberger, Comp. Meth. in Appl. Mech. and Eng., Vol. 197, Iss. 25-28, 15 April, pp. 2232-2249, (2008). [preprint PDF] Δ [full paper DOI]
Error Analysis of a Stochastic Immersed Boundary Method Incorporating Thermal Fluctuations, P.J. Atzberger and P.R. Kramer, Mathematics and Computers in Simulation, Vol. 79, Iss. 3, pg. 379 -- 408, (2008). [preprint PDF] Δ [full paper DOI]
A Stochastic Immersed Boundary Method for Fluid-Structure Dynamics at Microscopic Length Scales, P.J. Atzberger, P.R. Kramer, and C.S. Peskin, J. Comp. Phys., Vol. 224, Iss. 2, (2007). [preprint PDF Δ] [full paper DOI]
Stochastic Immersed Boundary Method Incorporating Thermal Fluctuations (brief introduction), P.J. Atzberger, P.R. Kramer, and C.S. Peskin, (proceedings of ICIAM 2007). [preprint PDF] Δ [full paper DOI]
Theoretical Framework for Microscopic Osmotic Phenomena, P.J. Atzberger and P.R. Kramer, Phys. Rev. E, 75, 1, (2007). [preprint PDF] Δ [full paper DOI]
A Note on the Correspondence of the Immersed Boundary Method with Thermal Fluctuations To Stokesian-Brownian Dynamics, P.J. Atzberger, Physica D, Vol. 226, Iss. 2, 15, pg. 144-150, (2007). [preprint PDF Δ] [full paper DOI]
Velocity Correlations of a Thermally Fluctuating Brownian Particle: A Novel Model of the Hydrodynamic Coupling, P.J. Atzberger, Phys. Lett. A, Vol. 351, Iss. 4-5, 6, March, pp. 225-230, (2006). [preprint PDF] Δ [full paper DOI]
A Brownian Dynamics Model of Kinesin in Three Dimensions Incorporating the Force-Extension Profile of the Coiled-Coil Cargo Tether, P.J. Atzberger and C.S. Peskin, Bull. Math. Biol., vol. 68, no. 1, pp. 131-160, (2006). [preprint PDF] Δ [full paper DOI]

We gratefully acknowledge the following sources of support:
Attach:NSF_dms_0956210.jpg Δ Attach:icb_logo2.gif Δ Attach:hellman3.png Δ Attach:NSF_dms_0635535.jpg Δ Attach:Keck_logo.jpg Δ
*This material is based upon work supported by the National Science Foundation under Grant No. NSF DMS-0635535 and NSF CAREER DMS-0956210. Any opinions, findings and conclusions or recomendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation (NSF).

Software

Stochastic Eulerian Lagrangian Method (SELM) : Pre-Release Mailing List

Stochastic Immersed Boundary Method (SIB) : Release 1.0 (alpha)

Class Websites and Course Notes:

  Course Notes and Resources:
  course notes and supplemental materials?

  Mathematical Finance Resources:
  course notes and supplemental materials

  Math Circle for Junior High School Students
  more information

  Ordinary Differential Equations and Linear Algebra (MATH3C) (Winter 2012)  
  TR 3:30pm - 4:45pm.
  course website

  Applied Stochastic Analysis (Fall 2011)  
  TR 9:30am - 10:45am.
  course website

  Finite Difference Methods for PDEs (Spring 2011)  
  TR 12:00pm - 1:45pm.
  course website

  Introduction to Real Analysis III (Spring 2011)  
  TR 11:00am - 12:15pm.
  course website

  Introduction to Real Analysis II (Winter 2011)  
  TR 11:00am - 12:15pm.
  course website

  Numerical Analysis II (Summer 2010)  
  TR 12:30pm - 1:35pm.
  course website

  Finite Difference Methods for Partial Differential Equations (Spring 2010)  
  TR 9:30am - 10:45am.
  course website

  Introduction to Mathematical Biology : Honors Seminar (Spring 2010)  
  T 11:00am - 12:20pm.
  course website

  Additional Class Websites:
  classes taught 2003 - present

Advising:

Postdoctoral Researchers:

Yaohong Wang
Erik Brandt

Graduate Students:

David Valdman
Pat Plunkett
Jon Karl Sigurdsson
Chia-Chun Fu (co-advisor)
Tom Wynne (co-advisor)

Undergraduate Students:

Gil Tabak

Former Students and Postdoctoral Researchers

Chetan Pahlajani
Justin Shrake
Daniel Kerr
Joe Rudzinski
Per Danzl (co-advisor)
Jordan Fischer (co-advisor)
Patrick Sheppard (co-advisor)

Administration:

Mathematical Finance Majors (Undergraduate Faculty Adviser)
Graduate Committee

Research Summary : Paul J. Atzberger

Research Areas:

Computational Fluid Dynamics
Molecular Biology
Bilayer Membranes with Protein Inclusions
Osmotic Phenomena
Numerical Methods for SPDEs

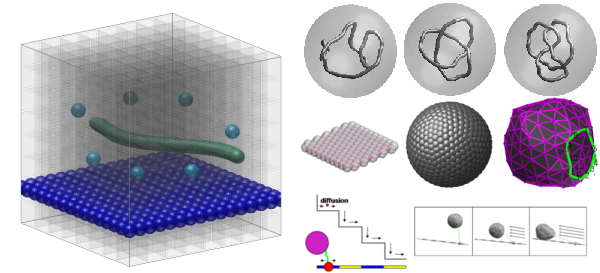
Computational Fluid Dynamics : Fluid-Structure Interaction : Stochastic Immersed Boundary Methods

The Stochastic Immersed Boundary Method (SIB) is a numerical approach for studying the mechanics of elastic structures which interact with a fluid in the presence of thermal fluctuations. The hydrodynamic interactions of the composite system are handled by an approximate treatment of the fluid-structure stresses. This approximation is expressed in terms of a Lagrangian representation of the immersed structures which is coupled to an Eulerian representation of the fluid. Thermal fluctuations are accounted for in the system by an appropriate stochastic forcing of the fluid-structure equations in accordance with the principles of statistical mechanics. The formalism is cast in terms of a system of Stochastic Partial Differential Equations (SPDE's). Fast time scales introduced into the fluid dynamics by the thermal fluctuations pose a challenge for conventional approaches to numerical approximation. Using results from stochastic calculus, we have developed efficient stochastic numerical methods for this formalism. We are currently extending this formalism to include more general coupling operators for approximation of the fluid-structure interactions with thermal fluctuations. This includes operators which allow for more general representations of immersed structures and which account for translational and rotational motions of immersed structures. We are also developing new stochastic numerical methods for non-periodic domains and adaptive multilevel meshes. For more details, see the papers and preprints below.

Attach:montage_sib.png Δ

⚠ (:area shape=rect coords=300,0,398,102 href=http://www.math.ucsb.edu/~atzberg/movies/unknot.avi:) ⚠ (:area shape=rect coords=398,0,499,102 href=http://www.math.ucsb.edu/~atzberg/movies/trefoilKnot.avi :) ⚠ (:area shape=rect coords=499,0,600,102 href=http://www.math.ucsb.edu/~atzberg/movies/figureEightKnot.avi :) ⚠ (:area shape=rect coords=300,103,398,187 href=http://www.math.ucsb.edu/~atzberg/movies/membraneSheet.avi" :) ⚠ (:area shape=rect coords=398,103,499,187 href=http://www.math.ucsb.edu/~atzberg/movies/membraneVesicle.avi" :) ⚠ (:area shape=rect coords=499,103,600,187 href=http://www.math.ucsb.edu/~atzberg/movies/membraneVesicleFormation.avi" :) ⚠ (:area shape=rect coords=414,205,473,253 href=http://www.math.ucsb.edu/~atzberg/movies/motor_no_load.avi" :) ⚠ (:area shape=rect coords=473,205,529,253 href=http://www.math.ucsb.edu/~atzberg/movies/motor_moderate_load.avi" :) ⚠ (:area shape=rect coords=529,205,600,253 href=http://www.math.ucsb.edu/~atzberg/movies/motor_large_load.avi" :)

Immersed structures in SIB can be used to represent the mechanics of a variety of microscopic hydrodynamic systems. We have applied the approach to a number of applications, see the figure above and movies below. In the context of complex fluids, immersed structures have been used to represent solute particles, polymers, or membrane structures. We have also extended the SIB approach to study the static and dynamic rheological responses of a number of complex fluids, see the papers below. In collaboration with Frank Brown, Department of Chemistry, dynamic coarse-grained models of lipid bilayer membranes are being developed using the SIB formalism to account for molecular level interactions, lipid-lipid and lipid-solvent hydrodynamic coupling, and thermal fluctuations, see the talks below.

Select Publications

Stochastic Eulerian-Lagrangian Methods for Fluid-Structure Interactions with Thermal Fluctuations, Atzberger, P.J., (2010), (preprint). [PDF] Δ
Simulation of Complex Fluids using Stochastic Eulerian Lagrangian Methods with Shear Boundary Conditions, Atzberger, P.J., (2010), (preprint). [PDF] Δ
Spatially Adaptive Stochastic Multigrid Methods for Fluid-Structure Systems with Thermal Fluctuations, Atzberger, P.J., (preprint), (2010). [PDF] Δ
A Stochastic Immersed Boundary Method for Fluid-Structure Dynamics at Microscopic Length Scales, Atzberger, P.J., Kramer, P.R., and Peskin, C.S., J. Comp. Phys., Vol. 224, Iss. 2, (2007). [PDF Δ] [DOI]
Stochastic Immersed Boundary Method Incorporating Thermal Fluctuations (brief introduction), Atzberger, P.J., Kramer, P.R., and Peskin, C.S., (proceedings of ICIAM 2007). [PDF] Δ [DOI]
A Note on the Correspondence of the Immersed Boundary Method with Thermal Fluctuations To Stokesian-Brownian Dynamics, Atzberger, P.J., Physica D, Vol. 226, Iss. 2, 15, pg. 144-150, (2007). [PDF Δ] [DOI]
On the Foundations of the Stochastic Immersed Boundary Method, Kramer, P.R., Peskin, C.S., and Atzberger, P.J., Comp. Meth. in Appl. Mech. and Eng., Vol. 197, Iss. 25-28, 15 April, pp. 2232-2249, (2008). [PDF] Δ [DOI]
Hybrid Elastic / Discrete-Particle Approach to Biomembrane Dynamics with Application to the Mobility of Curved Integral Membrane Proteins, Naji, A., Atzberger, P.J. and Brown, F.L.H., Phys. Rev. Lett. 102, 138102, (2009). [PDF] [DOI]

Movies for Select Simulation Results

Simulations of polymer knots showing SIB preservation of knot topology without the need for excluded volume interactions
- Unknotted Polymer [MPG] Δ
- Trefoil Knot [MPG] Δ
- Figure Eight Knot [MPG] Δ.
Simulations demonstrating a tethered membrane model using SIB for the hydrodynamic coupling
- Membrane Sheet [AVI]
- Membrane Vesicle [AVI]
- Membrane Vesicle Formation [AVI].
Simulations of motor protein transporting a cargo vesicle under an imposed hydrodynamic load
- No Load [AVI]
- Intermediate Load [AVI]
- Large Load [AVI].

⚠ <iframe title="YouTube video player" class="youtube-player" type="text/html" width="200" height="200" src="http://www.youtube.com/embed/-ipANLU7cCA?controls=0&hl=en&loop=1" controls="0" showinfo="0" frameborder="0" allowFullScreen> ⚠ </iframe> ⚠ <iframe title="YouTube video player" class="youtube-player" type="text/html" width="200" height="200" src="http://www.youtube.com/embed/_bDZx0AT8Bw?hl=en&fs=1&controls=0&loop=1" frameborder="0" allowFullScreen> ⚠ </iframe> ⚠ <iframe title="YouTube video player" class="youtube-player" type="text/html" width="200" height="200" src="http://www.youtube.com/embed/PyE2FX7eegs?hl=en&fs=1&controls=0&loop=1" frameborder="0" allowFullScreen> ⚠ </iframe>

⚠ <iframe title="YouTube video player" class="youtube-player" type="text/html" width="200" height="200" src="http://www.youtube.com/embed/jwIhZNA4-lI?hl=en&fs=1&controls=0&loop=1" frameborder="0" allowFullScreen> ⚠ </iframe> ⚠ <iframe title="YouTube video player" class="youtube-player" type="text/html" width="200" height="200" src="http://www.youtube.com/embed/9YDcSLB9nVM?hl=en&fs=1&controls=0&loop=1" frameborder="0" allowFullScreen> ⚠ </iframe> ⚠ <iframe title="YouTube video player" class="youtube-player" type="text/html" width="200" height="200" src="http://www.youtube.com/embed/gOkD2OofxbY?hl=en&fs=1&controls=0&loop=1" frameborder="0" allowFullScreen> ⚠ </iframe>

⚠ <iframe title="YouTube video player" class="youtube-player" type="text/html" width="200" height="200" src="http://www.youtube.com/embed/w61e1SElxzE?hl=en&fs=1&controls=0&loop=1" frameborder="0" allowFullScreen> ⚠ </iframe> ⚠ <iframe title="YouTube video player" class="youtube-player" type="text/html" width="200" height="200" src="http://www.youtube.com/embed/Ha8yIim4xJM?hl=en&fs=1&controls=0&loop=1" frameborder="0" allowFullScreen> ⚠ </iframe> ⚠ <iframe title="YouTube video player" class="youtube-player" type="text/html" width="200" height="200" src="http://www.youtube.com/embed/Y8LuFMALNqI?hl=en&fs=1&controls=0&loop=1" frameborder="0" allowFullScreen> ⚠ </iframe>

Return to Research Summary

Applications in Molecular Biology:

Experimental advances are yielding a wealth of quantitative information about the mechanics and localization of processes in cell biology. This is both at the level of single molecules and at more collective levels. This presents many opportunities for theoretical approaches to play a role in the study of biological systems. In collaboration with experimentalists on-campus at UCSB, we are working on several projects.

Motor Proteins:
Motor proteins act essentially as microscopic machines within cells to form cellular structures, transport materials, or generate forces. We are using stochastic modeling, analysis, and simulations to study the basic mechanisms underlying how molecular motor proteins may operate. In this work, we are making a particular effort toward building models for the analysis of specific experimental data sets. In previous work we have studied the kinesin motor protein and developed a coarse-grained mechanical model consistent with available optical trap experimental data, see paper. In current work, we are collaborating with the laboratory of Everett Lipman, Department of Physics, to study FRET signals which yield information about the dynamics of a single helicase motor protein as it moves along DNA. By considering both the helicase and DNA geometry along with the positioning of donar and acceptor dye molecules, we are studying models for the helicase dynamics consistent with experimental observations.

Attach:montage_molBio.png Δ

Microtubules:
Microtubules are long polymer filaments of the cytoskeleton that play many important roles in cell biology. This includes allowing cells to resist deformation during mechanical loading, serving as a highway for many types of motor proteins, and sustaining forces responsible for the separation of chromosomes during cell division. We are studying microtubule mechanics in collaboration with the laboratory of Megan Valentine, Department of Mechanical Engineering and the graduate student David Valdman, Department of Mathematics. In particular, we are studying how MAP proteins affect microtubule mechanics. One approach is based on the thermal fluctuations of microtubules observed through fluorescence microscopy. We are developing new approaches based on spectral analysis to infer elastic properties from observed thermal fluctuations. These methods are being used to develop new experimental assays to study how particular MAP proteins augment microtubule mechanical properties and to study biological consequences.

Aptamers:
We are studying Aptamers in collaboration with the laboratory of H.T. Soh, Department of Mechanical Engineering and undergraduate Joe Rudzinski (CCS Program, UCSB). Aptamers are short segments of DNA or RNA which bind to proteins. In applications, specific aptamers (nucleic acid sequences) are sought which bind to a desired target protein with high affinity and specificity. Applications include purification methods for proteins, analytics in biosensor devices, and target validation in pharmaceutical drug development. Obtaining aptamers with strong affinity and specificity binding a given target molecule poses a significant challenge in practice. We are developing mathematical approaches to study experimental methods for the selection of DNA-Aptamers from a library of random sequences.

Select Publications

Spectral Analysis Methods for the Robust Measurement of the Flexural Rigidity of Biopolymers, Valdman, D., Atzberger, P. J., Yu, D., and Valentine, M. T., (submitted), (2011). [PDF] Δ
Micromagnetic Selection of Aptamers in Microfluidic Channels, Lou, X., Qian, J., Yi, X., Viel, L., Gerdon, A.E, Lagally, E.T, Atzberger, P.J., Heeger, A.J., and Soh, H.T., PNAS, Vol. 106 No. 9 pp. 2989-2994, (2009), [DOI] [PDF]
Analysis of Selection Approaches for Aptamer Molecular Libraries, Rudzinski, J., Soh, T., Atzberger, P.J., (preprint) (2009), [PDF] Δ
Stochastic Reduction Method for Biological Chemical Kinetics using Time-Scale Separation, Pahlajani, C.D., Atzberger, P.J., Khammash, M. (2010), (preprint). [PDF] Δ
A Brownian Dynamics Model of Kinesin in Three Dimensions Incorporating the Force-Extension Profile of the Coiled-Coil Cargo Tether, Atzberger, P.J. and Peskin, C.S., Bull. Math. Biol., vol. 68, no. 1, pp. 131-160, (2006). [PDF] Δ [DOI]

Return to Research Summary

Fluctuating Lipid Bilayer Membranes with Diffusing Protein Inclusions : A Hybrid Continuum-Particle Approach

Lipid bilayer membranes appearing in biology and related experimental systems are often heterogeneous mixtures of lipid molecules and proteins. Many proteins through their geometry and specific interactions with lipids are thought to induce changes in the membrane material properties, which manifest in local stiffness variations and curvature. Consequently, as proteins diffuse within a bilayer, large-scale membrane features track with protein location. These interactions play an important role in the heterogeneous membrane mechanics and in the kinetics of membrane associated processes. To capture such effects, we have developed a hybrid continuum-particle description for the membrane-protein system that incorporates hydrodynamic coupling and thermal fluctuations. As an initial study we have investigated how protein curvature and membrane stiffness influence protein diffusion. We are also investigating how the area fraction of proteins influences membrane mechanical properties such as the elastic stiffness of the bilayer. Below are some recent simulation results.

⚠ <iframe width="283" height="212" src="http://www.youtube.com/embed/Kkh5KHcB7UQ?hd=1;fs=1;rel=0;showinfo=0;autohide=1" frameborder="0" allowfullscreen>⚠ </iframe> ⚠ <iframe width="283" height="212" src="http://www.youtube.com/embed/eEhZ_5FFLX4?hd=1;fs=1;rel=0;showinfo=0;autohide=1" frameborder="0" allowFullScreen>⚠ </iframe> ⚠ <iframe width="283" height="212" src="http://www.youtube.com/embed/gEC5e1stvFs?hd=1;fs=1;rel=0;showinfo=0;autohide=1" frameborder="0" allowfullscreen>⚠ </iframe>
On the left is shown a single curved protein diffusing within a membrane. The protein induces a local curvature that creates a membrane deformation that tracks with the protein location and influences significantly the protein diffusion. In the middle is shown a collection of flat proteins embedded within a lipid bilayer and how this influences the fluctuations of a membrane. Observation of the fluctuations along with spectral analysis can be used as a passive experimental measure of the effective membrane elasticity. On the right is shown a collection of proteins that induce significant local curvature in the membrane. This is seen to drive significant deformations in the shape of the membrane and alter the fluctuation spectrum. This work is being carried out in collaboration with F. Brown, Department of Chemistry and Physics and the graduate student Jon Karl Sigurdsson.

Select Publications

Fluctuating Lipid Bilayer Membranes with Diffusing Protein Inclusions : Hybrid Continuum-Particle Model, Sigurdsson, J. K., Atzberger, P.J. and Brown, F.L.H., (in preparation), (2011).
Hybrid Elastic and Discrete-Particle Approach to Biomembrane Dynamics with Application to the Mobility of Curved Integral Membrane Proteins, Naji, A., Atzberger, P.J. and Brown, F.L.H., Phys. Rev. Lett. 102, 138102, (2009). [PDF] [DOI]

Osmotic Phenomena

Osmosis refers to general phenomena in mechanical systems where pressures and forces are generated in a fluid or gas solvent by solute particles which are confined by semi-permeable membrane boundaries or electric fields. Such forces and pressures play a fundamental role in many biological systems and technological devices. Some examples in biology include mechanisms responsible for exchange of nutrients and wastes in microscopic capillaries in tissues and means of propulsion in cell motility. In technological applications, microscopic devices have been designed which utilize osmotic effects to pump fluids or utilize osmotic effects to actuate forces via swelling. The classical theories for osmotic pressure, such as van't Hoff's relation, become inaccurate for microscopic systems where solute particles interact on length scales comparable to the size of the confining chamber. Classical theories of osmosis also typically assume systems are in thermodynamic equilibrium.

Attach:montage_osmosis.png Δ

To study systems in regimes applicable to biological systems and microscopic devices we are developing theory to describe microscopic osmotic phenomena both in equilibrium and non-equlibrium settings. Some recent work includes studying how osmotic pressures generated by polymer solutes depend on polymer topology, stiffness, and excluded volume. In related work, a pumping mechanism for a microfluidic device has been proposed which uses reversible chemical reactions to drive fluid flows.

Select Publications

A Microfluidic Pumping Mechanism Driven by Non-equilibrium Osmotic Effects, Atzberger, P.J., Isaacson, S.A., and Peskin, C.S., Physica D: Nonlinear Phenomena, Vol. 238, Iss. 14, July, pp. 1168-1179, (2009),[PDF] Δ [DOI]
Theoretical Framework for Microscopic Osmotic Phenomena, Atzberger, P.J. and Kramer, P.R. , Phys. Rev. E, 75, 1, (2007). PDF] Δ [DOI]

Return to Research Summary

Stochastic Partial Differential Equations : Spatially Adaptive Numerical Methods

Stochastic partial differential equations (SPDEs) pose significant mathematical and computational challenges not present in the corresponding deterministic PDE setting. Solutions to SPDEs are often not classical requiring instead a measure on a space of generalized functions (distributions). These features pose significant challenges for the numerical approximation of SPDEs. Often spectral methods are employed but this usually requires periodic boundary conditions or domains of rather simple geometry. We are developing alternative finite difference numerical methods for the approximation of SPDEs utilizing ideas from statistical mechanics. Our approach allows for general boundary conditions, complex domain geometries, and the use of adaptive spatial meshes. A key challenge these methods address for adaptive meshes is to properly treat the stochastic driving terms at the coarse-refined interfaces.

As a demonstration we present results for a stochastic reaction-diffusion system with two chemical species undergoing Gray-Scott reactions subject to intrinsic concentration fluctuations. The results show the evolution of a stochastically induced spatial pattern which does not occur in the absence of fluctuations. Our methods utilize a quad-tree adaptive refinement mesh which dynamically changes as corresponding spatial regions become chemically active.

Attach:montage_reactionDiffusion.png Δ

Growth of a noise-induced spatial pattern resolved with adaptive meshing [AVI Movie].

An important feature of the stochastic numerical methods is how the the stochastic driving field is treated at the coarse-refined interface. For a purely diffusive system the equilibrium fluctuations in concentration are essentially spatially uncorrelated at any instant. At coarse-refined interfaces the discretization of the stochastic driving field may introduce artificial long-range spatial correlations. Below is shown the resulting equilibrium covariance structure of fluctuations with the mesh site marked +. Results are shown for the cases corresponding to a white-noise discretized stochastic driving field, a discretized stochastic driving field derived from random fluxes, and our discretized stochastic driving field. To derive consistent discretizations of the stochastic driving field at coarse-refined interfaces, we use notions related to the fluctuation-dissipation principle of statistical mechanics. We are using these approaches to develop a variety of stochastic numerical methods for the study of spatially extended stochastic systems.

Attach:reactionDiffusion_coarseRefinedInterfaces.png Δ

Select Publications

Spatially Adaptive Stochastic Numerical Methods for Intrinsic Fluctuations in Reaction-Diffusion Systems, Atzberger, P.J., (Journal of Computational Physics, Volume 229, Issue 9, 1 May, Pages 3474-3501, (2010). [PDF] Δ [DOI]
Spatially Adaptive Stochastic Multigrid Methods for Fluid-Structure Systems with Thermal Fluctuations, Atzberger, P.J., (preprint), (2010). [PDF] Δ

Movies for Select Simulation Results

Fluctuation-induced spatial pattern resolved with adaptive meshing: [AVI Movie].

⚠ <iframe title="YouTube video player" class="youtube-player" type="text/html" width="200" height="200" src="http://www.youtube.com/embed/71XJLArjPTs?hl=en&fs=1&controls=0&loop=1" frameborder="0" allowFullScreen> ⚠ </iframe>

Return to Research Summary

For a more in-depth discussion of this work and information about additional projects please see the publications section.