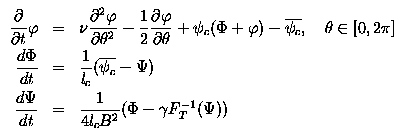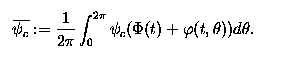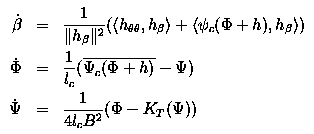In recent years a lot of attention has been devoted
to the study of air flow through turbomachines. The main reason for
this interest is that when a turbomachine, such as a jet engine, operates
close to its optimal operating parameter values, the flow can become unstable.
These instabilities put a large stress on the engine and in some cases
the engine needs to be turned off in order to recover original operation.
For this reason jet engines are currently operated away from their optimal
operating parameter values increasing both fuel consumption and the engine
weight.
A jet engine can be thought of as a compressor, where
the incoming air is compressed by alternating rings of rotating blades
and stationary blades. The mixture of fuel and compressed air is
then ignited and the resulting combustion generates thrust that propels
the aircraft. This is better explained by a picture, for a more detailed
description of how the engine works click here.
There are primarily two types of instabilities that occur in the flow through
the compressor. They are called surge and stall. Surge
is characterized by large oscillations of the mean mass flow through the
engine. During part of the cycle, the mean mass flow may become reversed,
thrusting air out the front of the engine. This puts a large stress
on the components of the engine and seriously impairs its performance.
When stall occurs, there are regions of relatively
low air flow that form at isolated locations around the rim of the compressor.
Here too, the phenomenon can be so pronounced that the flow in these isolatedregions
is reversed. Again this causes a large stress on the components of
the engine and reduces its performance.
Moore and Greitzer published in 1986 a pde model describing
the airflow through the compression system in turbomachines. Although
relatively simple, this model has been surprisingly succesful at predicting
experimental outcomes. Currently Mezic has derived a model of the
three dimensional flow in jet engine compressors. In his treatment,
a diffusive term, first introduced by Adomaitis and Abed, is justified
and interpreted as the inviscid process of turbulent momentum transport
via Reynolds stresses. It is this model with the additional assumption
that the flow has no radial component that we analyze. In this guise
it is called the viscous Moore-Greitzer equation (vMG).
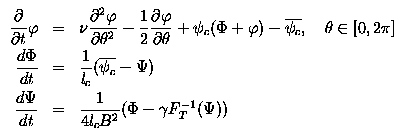 where
where
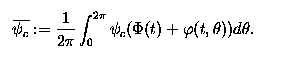
The vMG equation is a nonlinear nonlocal parabolic partial
differential equation on the unit circle that is coupled with two ordinary
differential equations. The two odes describe the average flow through
the compressor and the pressure rise from atmospheric pressure to the pressure
in the plenum. The pde describes the deviations of the flow from
the average flow. The parameter gamma
is called the throttle parameter and this will later be our control parameter.
The majority of previous research in this area has been
focused on a simple Galerkin projection of the Moore-Greitzer equation,
namely assuming that the solution of the pde is the first Fourier mode
with a varying amplitude. Some simple extensions of this have also
been considered, such as projecting onto more than one Fourier mode or
a linear combination of Fourier modes. One exception from this is
a control result by Banaszuk, Hauksson and Mezic for the full Moore-Greitzer
model.
Our first results in this area were to prove
the existence and uniqueness of solutions of the vMG equation. Furthermore,
the solutions are smooth in positive time and the equation has a global
attractor. We found explicit bounds on the fractal and Hausdorff
dimensions of this attractor, but as is frequently the case for these type
of bounds, they were fairly large. Analysis of the attractor, or
more precise the basic attractor, shows that its structure is not too complicated.
The basic attractor is the smallest part of the attractor which attracts
all of state space with probability one. In simple systems it can
be thought of as all the stable orbits in the global attractor.
The basic attractor consists of design flow, surge and
one or more stall solutions. The design flow is a stationary solution
and surge is a periodic orbit in the two ode variables, average flow and
pressure rise. Surge, being a two dimensional phenomenon, has for
the most part been understood. Stall, on the other hand, has until
now only been analyzed in low order Galerkin projections.
By assuming that stall is a traveling wave one can use
Hamiltonian methods to prove the existence of finitely many stall solutions.
In fact, one can find an explicit expression for them and they are given
as rational functions of the Jacobi elliptic function ns.
These stall solutions are solitons that rotate around the annulus and depending
on the parameters one can have one pulse solutions up to N pulse solutions.
Furthermore, when one linearizes the vMG equation about a stall solution,
there exists a beautiful relationship between the resulting linear operator
and the Schrodinger equation with Lame potential. This in fact allows
us to find explicitly the first eigenvalues and eigenvectors of the linearized
operator as well as characterizing the rest of the spectrum. It turns
out that the stall solutions are stable over a large parameter range and
hence belong to the basic attractor.
When one varies the parameter gamma
then the shape of the stall cells changes and in fact each stall solution
is a member of a one parameter family of stall solutions. The one
parameter family for the one pulse solution is shown in Figure 1.
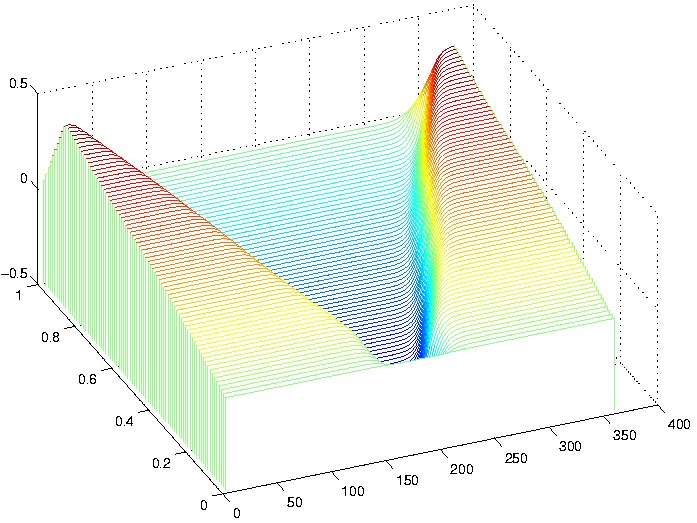
Figure 1: On the horizontal axis is the angular position
around the annulus, on the vertical one the deviation of the flow from
the average flow and on the axis going into the picture we vary a parameter
that allows us span the whole family. Notice that for the most part
it is the width of the stall cell that is changing with the parameter,
but not its amplitude.
Here we also display a movie that shows how stall evolves
from a small disturbance to design flow. Stall
evolution (4 Mb)
Reduced Order Model and Control
A primary goal of the current jet engine research
is to understand the flow better and to be able to control the flow through
the engine. In order to facilitate this goal, a meaningful model
reduction is needed. The Galerkin approximations have been able to
describe many aspects of the flow qualitatively, but not quantitatively.
For this a better model reduction is needed. It has been suggested to make
a Galerkin approximation with a more general basis than the Fourier basis
and some results have been obtained using multiple Fourier modes.
The disadvantage of making a Galerkin truncation onto
a function with a fixed spatial shape is that it doesn't describe properly
how the stall cells seem to grow and decay in simulations (see the movie
here above). What one observes there is that the stall cell quickly
develops a square like spatial structure with a fixed depth. This
square structure then widens until it stabilizes at a fixed width or it
fills the whole annulus of the compressor which goes into surge.
To capture this behaviour with modes of fixed spatial shape one needs to
include many modes and the behaviour of the amplitudes of these modes can
be very complicated. A remedy for this is to try to capture the dynamics
with a one parameter family of curves. The parameter then determines
not only the amplitude, but also the shape of the
stall cell. We have indeed been able to create a reduced order model
in this fashion by assuming that the solution of the pde is given by a
function h(omega, t-0.5*theta) where the parameter
omega is timedependent. The equations
for this model are
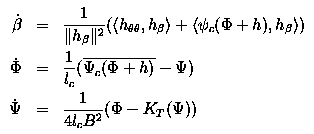
Here subscripts denote partial derivatives and the pointed
brackets the inner product. This model captures remarkably well the
dynamics of the vMG equation. It captures both asymptotic behavior
as well as transient behavior both qualitatively and quantitatively.
This would indicate that the one parameter family of stall cells is very
strongly attracting. On the figure here below we see the transient
behavior as the engine goes into stall. The solid curve is from the
reduced order model while the dotted one is from the pde simulations.
This shows that the reduced order is quantitatively right on the mark.
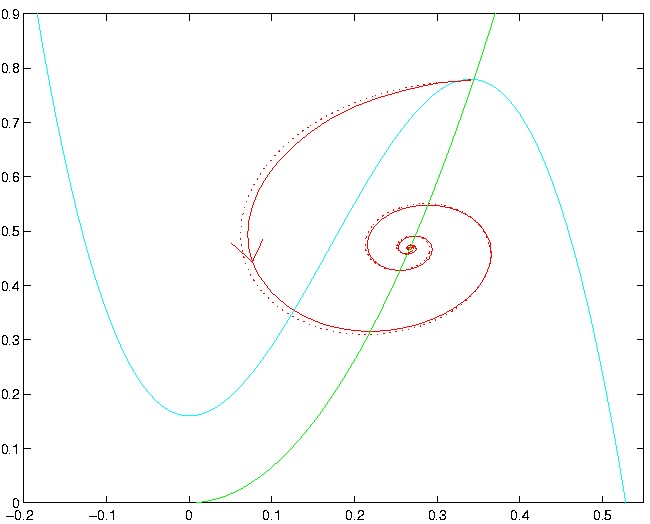
Figure 2: The vertical axis is pressure rise and the
horizontal axis is average flow. The blue line shows the compressor
characteristic and the green one the throttle characteristic. Design
flow is where these two curves intersect. We see here how a small
disturbance from design flow gives rise to a transient that spirals towards
a stall solution. The solid line is calculated by the reduced order
model and the dotted one by simulating the pde. The aggreement between
the two models is strikingly good.
This reduced order model can be extended to include also
soliton solutions with more than one pulse in a trivial way. Dan
Fontain and Petar Kokotovic have used a simple approximation to this model,
where the one parameter family is approximated by a one parameter family
of trapezoidal shapes, with good success.
Armed with this reduced order model, we can now study
the dynamics in more detail. In particular, we can analyze the bifurcations
of stall solutions and Figure 3 shows the branches for the one pulse stall
solution in the average flow-pressure rise plane. The parameter that
one varies here is gamma. For a large
enough gamma there don't exist any stall solutions. As gamma is decreased,
there occurs a saddle-node bifurcation and two one pulse stall solutions
are created, one stable and one unstable. The branch for the stable
one is denoted by the flat blue curve on Figure 3 and the branch for the
unstable one is the red dotted line. The stable stall solution persists
for a large parameter range, but collides eventually with another unstable
stall solution and vanishes.
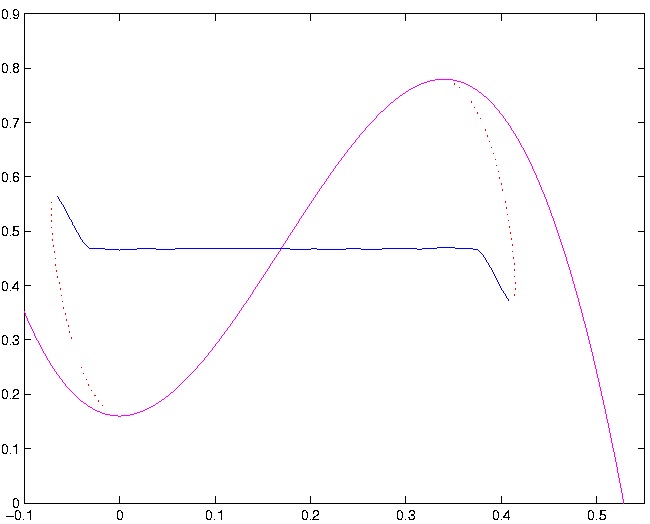
Figure 3: This figure shows the bifurcation diagram for
one pulse stall solutins. The axis are the same as above. The
flat blue curve is the branch for the stable stall solutions and the red
dotted curves are the branches for the unstable stall solutions.
In normal operation of the engine, one can make a regulator
keep the flow close to design flow, but as we saw in Figure 2, under certain
circumstances even small disturbances can cause the engine to stall.
Therefore, a control strategy to recover from stall is needed. Banaszuk,
Hauksson and Mezic constructed a controller for the Moore-Greitzer equation
which recovers design flow for any initial conditions. This controller
is however not very cost effective, in particular, it over reacts to small
amplitude high frequency disturbances. Furthermore, they considered
the inviscid Moore-Greitzer equation, which is a hyperbolic equation, and
it doesn't have the same asymptotic properties as the vMG equation.
Current results by Mezic have shown that the vMG model is a better physical
model for the jet engine than the inviscid Moore-Greitzer equation.
Our goal is to construct a controller which is in some
sense near optimal by using our analysis of the asymptotic dynamics.
Let us assume for now that the control parameter gamma
can only be changed adiabatically. In this case the basic attractor,
which attracts all of state space with probability one, will remain unchanged.
I.e. it consists of stall solutions, surge and design flow. In this
case, any control strategy that doesn't make gamma
large enough so that the throttle characteristic doesn't intersect any
stall branch while the system is in stall, will fail to recover design
flow because the stall solution will persist. If on the other hand,
one makes gamma large enough so that there
is no intersection, then all of state space is attracted to the design
flow. Our control strategy will then be to make gamma
large enough when the system is in stall or surge so that it we will recover
design flow. This design flow is however at a low pressure rise and
one would want to operate closer to the peak of the compressor characteristic.
To obtain this goal, we propose to now track a trajectory from our current
design flow setting along the characteristic to our desired design flow
setting. By linearizing the vMG equation about this curve the problem
of tracking the problem in an optimal way with respect to quadratic cost
can be written as a servo-mechanism problem with quadratic cost.
It turns out that this problem can be reduced to solving five odes to obtain
the optimal feedback control. This control strategy is depicted in
Figure 4.
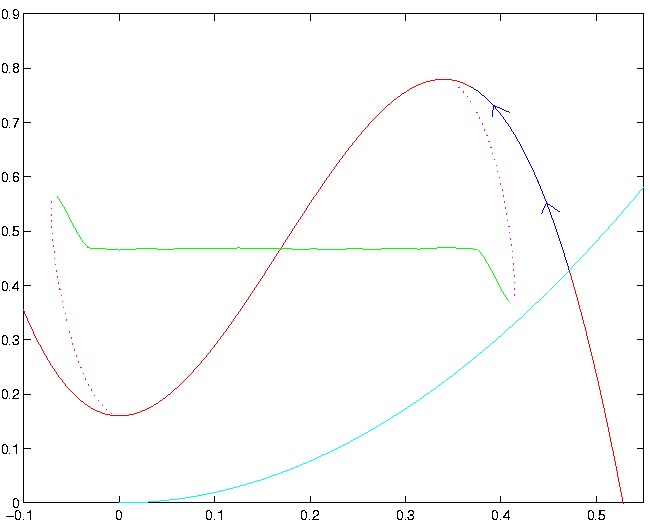
Figure 4: This figure shows the control strategy for
the adiabatic control. First one increases the control parameter
so that the throttle characteristic doesn't intersect the stall solution
branch, and then one tracks a trajectory along the compressor characteristic
to the desired design flow setting in an optimal way.
Although we have now found the optimal adiabatic control
strategy for recovering design flow, it is clearly not optimal to restrict
ourselves to adiabatic controls. The transient behavior of the system
appears however to die out fairly fast in simulations and in experimets.
This would indicate that when one considers all controls that change the
control parameter gamma at moderate rates,
the above control strategy should be close to the optimal strategy.
It is in this sense that we claim that our control strategy is near optimal.
A simulation of the vMG with the near optimal control strategy can be seen
in this movie.
Aknowledgements:
We would like to thank Petar Kokotovic, Igor Mezic, Andrzej
Banaszuk and Dan Fontain for fruitful discussions