Let \(s_i\) denote the score of the \(i\)th frolf player, and define \(B\) as the best score, and \(W\) as the worst score. I assign a rank to each player \(i\):
\[r_i = \frac{s_i-W}{B-W}.\]
When \(B=W\), I just set \(r_i\equiv 1\). Note that the first time we played, I ranked players based on their position, and not their score. Yoshi suggested the score-based ranking, and I agreed that it seemed to make more sense.
Let \(P\) denote the set of all power-ups. For each power-up \(p\in P\), there is an associated positive weight function \(W_p(r)\) which takes as input a player's rank, and outputs the corresponding weight for the power-up \(p\). So I defined the probability of player \(i\) receiving power \(p\) as:
\[\mathbb{P}(\text{player }i\text{ recieves power }p) = \frac{W_p(r_i)}{Z(r_i)},\]
Where \(Z(r) = \sum_{x\in P}W_x(r)\) is a normalization factor. Since basically everything in the universe can be described with a Gaussian distribution, I went ahead and made all the weight functions Gaussian, that is,
\[W_p(r) = M_p\exp\left(-\frac{(x-\mu_p)^2}{2\sigma_p^2}\right).\]
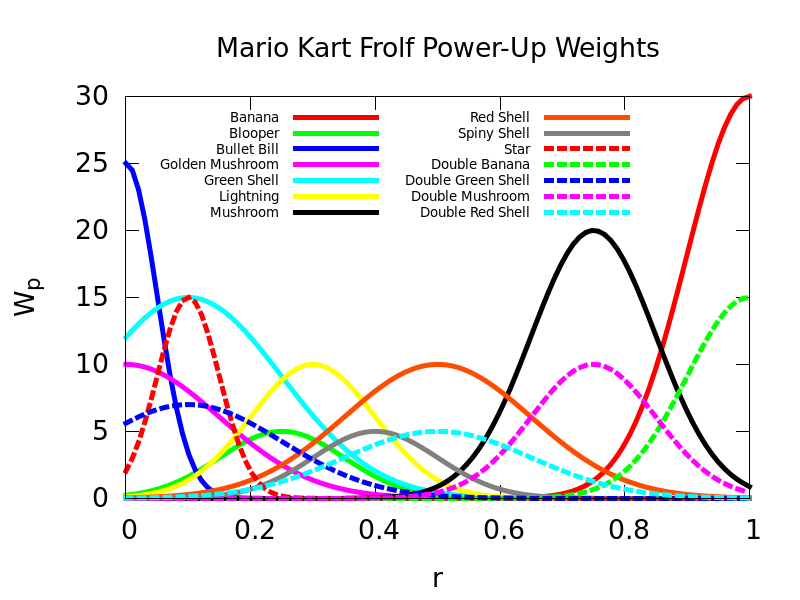
Here's a table of all the \(M_p\), \(\mu_p\), and \(\sigma_p\) values:
| \(M_p\) | \(\mu_p\) | \(\sigma_p\) | |
|---|---|---|---|
| Banana | 30 | 1.00 | 0.10 |
| Blooper | 5 | 0.25 | 0.10 |
| Bullet Bill | 25 | 0.00 | 0.05 |
| Golden Mushroom | 10 | 0.00 | 0.15 |
| Green Shell | 15 | 0.10 | 0.15 |
| Lightning | 10 | 0.30 | 0.10 |
| Mushroom | 20 | 0.75 | 0.10 |
| Red Shell | 10 | 0.50 | 0.15 |
| Spiny Shell | 5 | 0.40 | 0.10 |
| Star | 15 | 0.10 | 0.05 |
| Double Banana | 15 | 1.00 | 0.10 |
| Double Green Shell | 7 | 0.10 | 0.15 |
| Double Mushroom | 10 | 0.75 | 0.10 |
| Double Red Shell | 5 | 0.50 | 0.15 |
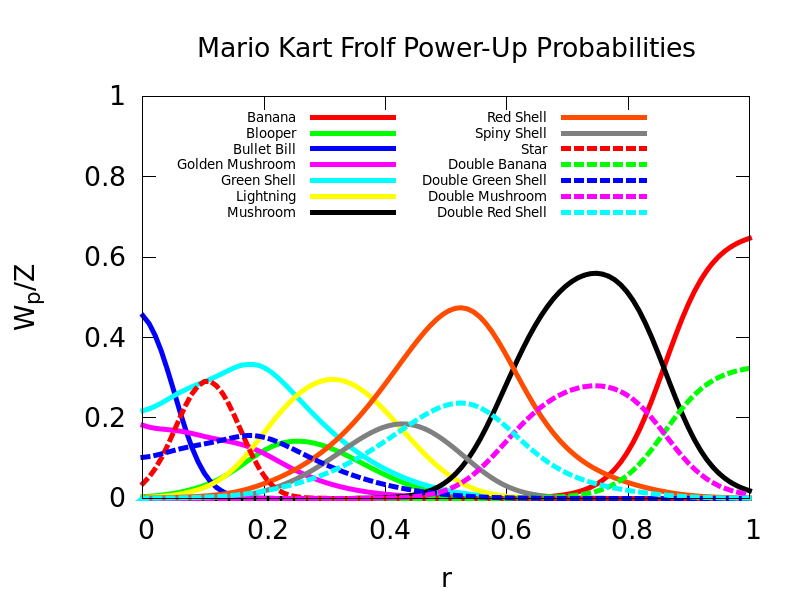
From here, it is useful to look at a plot of the weight functions for all powers (note that \(r=1\) corresponds to first place, and \(r=0\) corresponds to last place):
It might be useful to also look at the actual probabilities, instead of just the weights: