Professor Paul J. Atzberger : Atzberger Group Intranet Pages

Description

Welcome to the class website for Machine Learning: Special Topics . This graduate seminar course covers special topics in machine learning aiming to develop materials from the perspective of mathematical foundations and theory behind learning algorithms as well as discussing practical computational aspects and applications. Please check back for updates as new information may be posted periodically on the course website.

We plan to use the books

The Elements of Statistical Learning: Data Mining, Inference, and Prediction, by Hastie, Tibshirani, Friedman.
Foundations of Machine Learning, by Mehryar Mohri, Afshin Rostamizadeh, and Ameet Talwalkar.

The course will also be based on recent papers from the literature and special lecture materials prepared by the instructor. Topics may be adjusted based on the backgrounds and interests of the class.

Syllabus [PDF]

Topic Areas

Foundations of Machine Learning / Data Science
- Historic developments and recent motivations.
- Concentration Inequalities and Sample Complexity Bounds.
- Statistical Learning Theory, PAC-Learnability, related theorems.
- Rademacher Complexity, Vapnik–Chervonenkis Dimension.
- No-Free-Lunch Theorems.
- High Dimensional Probability and Statistics.
- Optimization theory and practice.
Supervised learning
- Linear methods for regression and classification.
- Model selection and bias-variance trade-offs.
- Support vector machines.
- Kernel methods.
- Parametric vs non-parametric regression.
- Neural network methods: deep learning.
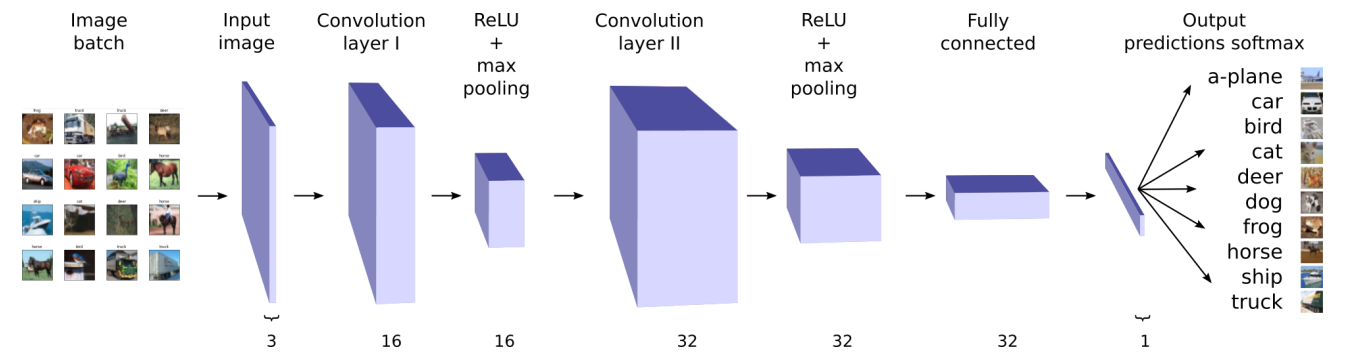
- Convolutional Neural Networks (CNNs).
- Recurrent Neural Networks (RNNs).
Unsupervised learning
- Clustering methods
- Kernel principal component analysis, and related methods
- Manifold learning
- Neural network methods.
- Autoencoders (AEs)
- Generative Adversarial Networks (GANs)
Additional topics
- Stochastic approximation and optimization.
- Variational inference.
- Generative Methods: GANs, AEs.
- Graphical models.
- Randomized numerical linear algebra approximations.
- Dimensionality reduction.

Prerequisites:

Linear Algebra, Probability, and ideally some experience programming.

Slides

Statistical Learning Theory, Generalization Errors, and Sampling Complexity Bounds: [Large Slides] [PDF] [MicrosoftSlides]
⚠ <iframe src="https://onedrive.live.com/embed?cid=85808E8A085197E0&resid=85808e8a085197e0%215696&authkey=AH8ZKxc54xQWzjc&em=2&wdAr=1.7777777777777777" width="350px" height="221px" frameborder="0">This is an embedded ⚠ <a target="_blank" href="https://office.com">Microsoft Office⚠ </a> presentation, powered by ⚠ <a target="_blank" href="https://office.com/webapps">Office⚠ </a>.⚠ </iframe>

Complexity Measures, Radamacher, VC-Dimension: [Large Slides] [PDF] [MicrosoftSlides]
⚠ <iframe src="https://onedrive.live.com/embed?cid=85808E8A085197E0&resid=85808E8A085197E0%215707&authkey=AKd1Oh949encoKY&em=2&wdAr=1.7777777777777777" width="350px" height="221px" frameborder="0">This is an embedded ⚠ <a target="_blank" href="https://office.com">Microsoft Office⚠ </a> presentation, powered by ⚠ <a target="_blank" href="https://office.com/webapps">Office⚠ </a>.⚠ </iframe>

Support Vector Machines, Kernels, Optimization Theory Basics: [Large Slides] [PDF] [MicrosoftSlides]
⚠ <iframe src="https://onedrive.live.com/embed?cid=85808E8A085197E0&resid=85808E8A085197E0%215710&authkey=ANymYB4ubCzxuV8&em=2&wdAr=1.7777777777777777" width="350px" height="221px" frameborder="0">This is an embedded ⚠ <a target="_blank" href="https://office.com">Microsoft Office⚠ </a> presentation, powered by ⚠ <a target="_blank" href="https://office.com/webapps">Office⚠ </a>.⚠ </iframe>

Regression, Kernel Methods, Regularization, LASSO, Tomography Example: [Large Slides] [PDF] [MicrosoftSlides]
⚠ <iframe src="https://onedrive.live.com/embed?cid=85808E8A085197E0&resid=85808E8A085197E0%215712&authkey=ACOk5uGNKWdw7xk&em=2&wdAr=1.7777777777777777" width="350px" height="221px" frameborder="0">This is an embedded ⚠ <a target="_blank" href="https://office.com">Microsoft Office⚠ </a> presentation, powered by ⚠ <a target="_blank" href="https://office.com/webapps">Office⚠ </a>.⚠ </iframe>

Unsupervised Learning, Dimension Reduction, Manifold Learning: [Large Slides] [PDF] [MicrosoftSlides]
⚠ <iframe src="https://onedrive.live.com/embed?cid=85808E8A085197E0&resid=85808E8A085197E0%215718&authkey=AJw9agZaP0r4iU0&em=2&wdAr=1.7777777777777777" width="350px" height="221px" frameborder="0">This is an embedded ⚠ <a target="_blank" href="https://office.com">Microsoft Office⚠ </a> presentation, powered by ⚠ <a target="_blank" href="https://office.com/webapps">Office⚠ </a>.⚠ </iframe>

Neural Networks and Deep Learning Basics: [PDF] [GoogleSlides]
⚠ <iframe src="https://docs.google.com/presentation/d/e/2PACX-1vQ_qqlIeqDCveAd_q1SIa7PVQPzK5S0jveZPnm3QPVX_tdUK-51PIAEt5QO7qHz6w7LyM3re7-AJ3kF/embed?start=false&loop=false&delayms=3000" frameborder="0" width="320" height="197" allowfullscreen="true" mozallowfullscreen="true" webkitallowfullscreen="true">⚠ </iframe>

Convolutional Neural Networks (CNNs) Basics: [PDF] [GoogleSlides]
⚠ <iframe src="https://docs.google.com/presentation/d/e/2PACX-1vRkrt9kmOf4D0TfKoCt5DVzRlVAchCIj2wvuNQTnoNxItsEu-qwZYb3T_Z3_wuomnYd_YtpnPl9fv8X/embed?start=false&loop=false&delayms=1000" frameborder="0" width="320" height="197" allowfullscreen="true" mozallowfullscreen="true" webkitallowfullscreen="true">⚠ </iframe>

Recurrent Neural Networks (RNNs) Basics: [Large Slides] [PDF] [MicrosoftSlides]
⚠ <iframe src="https://onedrive.live.com/embed?resid=85808E8A085197E0%215716&authkey=%21AAyyzfc4iBhjNiQ&em=2&wdAr=1.7777777777777777" width="350px" height="221px" frameborder="0">This is an embedded ⚠ <a target="_blank" href="https://office.com">Microsoft Office⚠ </a> presentation, powered by ⚠ <a target="_blank" href="https://office.com/webapps">Office⚠ </a>.⚠ </iframe>

Generative Adversarial Networks (GANs): [Large Slides] [PDF] [MicrosoftSlides]
⚠ <iframe src="https://onedrive.live.com/embed?cid=85808E8A085197E0&resid=85808E8A085197E0%215720&authkey=AIyvDv2tTyTYsFc&em=2&wdAr=1.7777777777777777" width="350px" height="221px" frameborder="0">This is an embedded ⚠ <a target="_blank" href="https://office.com">Microsoft Office⚠ </a> presentation, powered by ⚠ <a target="_blank" href="https://office.com/webapps">Office⚠ </a>.⚠ </iframe>

Exercises:

Problem Set 1: [PDF]
Problem Set 2: [PDF]
Problem Set 3: [PDF]
Problem Set 4: [PDF]
Image Classification using Convolutional Neural Networks

Supplemental Materials:

Additional Materials

You can find additional materials on my related data science course websites