
|
Homepage |
Description
Welcome to the class website for Machine Learning: Foundations and Applications . This course will cover select topics in machine learning concerning mathematical foundations and practical aspects for use on diverse applications. The class will also cover select advanced topics on deep learning and dimension reduction. Please check back here for updates as new information may be posted periodically on the course website.
We plan to use the books
- The Elements of Statistical Learning: Data Mining, Inference, and Prediction, by Hastie, Tibshirani, Friedman.
- Foundations of Machine Learning, by Mehryar Mohri, Afshin Rostamizadeh, and Ameet Talwalkar.
The course will also be based on recent papers from the literature and special lecture materials prepared by the instructor. Topics may be adjusted based on the backgrounds and interests of the class.
Syllabus [PDF]
Topics
- Introduction and discussion of background for machine learning / data science.
- Historic developments and recent motivations
- Statistical Learning Theory, PAC-Learnability, related theorems
- Rademacher Complexity, Vapnik–Chervonenkis Dimension
- Concentration Inequalities and Sample Complexity Bounds
- No-Free-Lunch Theorems
- Motivating applications
- Optimization theory and practice
- Supervised learning
- Linear methods for regression and classification
- Model selection and bias-variance trade-offs
- Support vector machines
- Kernel methods
- Parametric vs non-parametric regression
- Graphical models
- Neural network methods
- Unsupervised learning
- Clustering methods
- Principle component analysis and related methods
- Manifold learning
- Kernel methods
- Neural network methods
- Additional topics
- Deep Learning Methods
- Neural Network Architectures, Training, Regularization
- Stochastic gradient descent
- First-order non-linear optimization methods
- Markov-Chain Monte-Carlo (MCMC) sampling for posterior distributions
- Sampling with ito stochastic processes
- Variational inference
- Iterative methods and preconditioning
- Dimensionality reduction
- Sparse matrix methods
- Stochastic averaging and multiscale methods
- Example applications
Prerequisites:
Calculus, linear algebra, and ideally some experience programming.
Grading:
The grade for this special topics class will be based on participation and through specific homework assignments and a final project.
Supplemental Materials:
- Python tutorial at Codecademy.
- Python 2.7 documentation.
- Python 3.6 documentation.
- Enthought Canopy integrated analysis environment.
- Numpy Tutorial
- Anaconda Tutorial
Statistical Learning Theory, Generalization Errors, and Sampling Complexity Bounds: [PDF] [GoogleSlides]
⚠ <iframe src="https://docs.google.com/presentation/d/e/2PACX-1vQ0h3Fwd_DyX2TJiBW1ccgnzF8r3td2949C6sbOFt9EJJL1_nB5LmVa7hsclYMRKIsogTy4GDIZCjfj/embed?start=false&loop=false&delayms=3000" frameborder="0" width="320" height="197" allowfullscreen="true" mozallowfullscreen="true" webkitallowfullscreen="true">⚠ </iframe>
Neural Networks and Deep Learning Basics:
[PDF] [GoogleSlides] ⚠ <iframe src="https://docs.google.com/presentation/d/e/2PACX-1vQ_qqlIeqDCveAd_q1SIa7PVQPzK5S0jveZPnm3QPVX_tdUK-51PIAEt5QO7qHz6w7LyM3re7-AJ3kF/embed?start=false&loop=false&delayms=3000" frameborder="0" width="320" height="197" allowfullscreen="true" mozallowfullscreen="true" webkitallowfullscreen="true">⚠ </iframe>
Convolutional Neural Networks (CNNs) Basics:
[PDF]
[GoogleSlides]
⚠ <iframe src="https://docs.google.com/presentation/d/e/2PACX-1vRkrt9kmOf4D0TfKoCt5DVzRlVAchCIj2wvuNQTnoNxItsEu-qwZYb3T_Z3_wuomnYd_YtpnPl9fv8X/embed?start=false&loop=false&delayms=1000" frameborder="0" width="320" height="197" allowfullscreen="true" mozallowfullscreen="true" webkitallowfullscreen="true">⚠ </iframe>
Homework Assignments:
Turn all homeworks into South Hall 6th Floor by 5pm on the due date. Homeworks will be returned in class.
HW1: (Due Tuesday, October 9th) [PDF]
Kaggle1: (Due Thursday, October 18th) Linear Regression (warm-up) [Python Code]
HW2: (Due Thursday, October 25th) [PDF]
Kaggle2: (Due Thursday, November 8th) [Kaggle PDF]
Digit Classification MNIST (k-NN)
HW3: (Due Wednesday, November 21st) [PDF]
Kaggle3: (Due Tuesday, November 27th) [Kaggle PDF] Facial Recognition (SVM)
Facial Recognition Codes: [Jupyter Notebook PDF]
[Jupyter Notebook Code]
[data-folder]
HW4: (Due Thursday, November 29th) [PDF]
HW5: (Due Thursday, December 6th) [PDF]
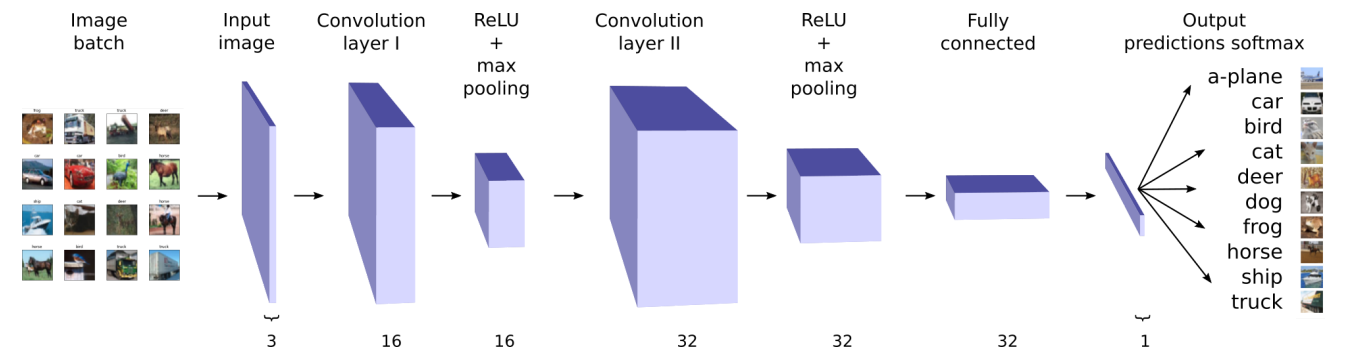
Kaggle4: (Due Tuesday, December 11th) [Kaggle PDF] Image Classification: Convolutional Neural Networks (CNNs)
Neural Network Codes: [Jupyter Notebook CIFAR10 PDF] [Jupyter Notebook MNIST PDF]
[Jupyter Notebook Codes] [data-folder]
Coding Exercises
- Facial Recognition and Feature Extraction

- Image Classification using Convolutional Neural Networks
Additional Materials
- You can find additional materials on my related data science course websites