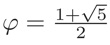PREVIOUS                HOME                NEXT

We can rewrite Ramanujan’s continued fraction identities as follows:

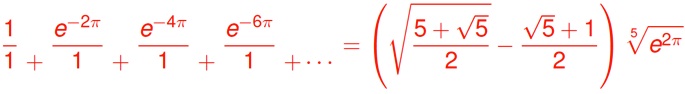
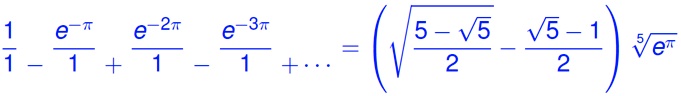
Take                      for τ in the complex upper half plane, and define

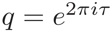
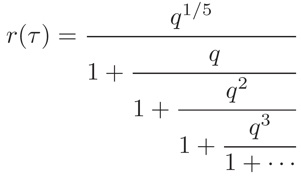
Ramanujan’s identities are equivalent to the following equations:

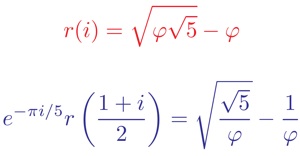
Here                     is the golden ratio. The key to proving the above equalities is a transformation property of the function r(τ) which we will see can be interpreted as a statement of modularity up to the symmetries of a Platonic solid having twenty faces.