PREVIOUS                HOME                NEXT

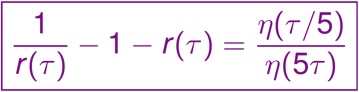
Define the Dedekind eta function by

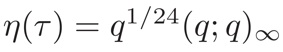
where the q-Pochhammer symbol is given by the product

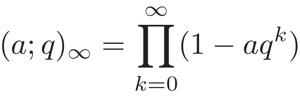
Then we have the following Key Result:

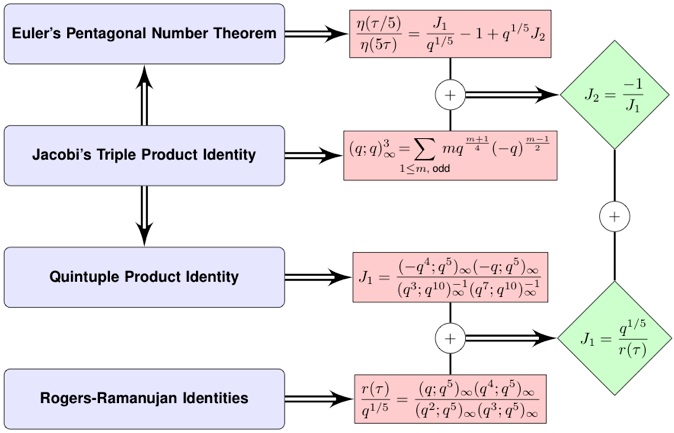
This result is proven by combining several combinatorial and algebraic identities. The components in the proof are outlined in the flowchart below.

The most crucial piece in the proof is the pair of Rogers-Ramanujan identities. These are algebraic expressions of deep combinatorial facts; e.g., one of the identities is equivalent to the statement that for every positive integer n the number of partitions of n into parts with minimal difference two is equal to the number of partitions of n into parts which congruent to 1 or 4 modulo 5. For n = 6, we have 1 + 5 = 2 + 4 = 6 and 1 + 1 + 1 + 1 + 1 + 1 = 1 + 1 + 4 = 6.