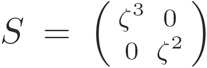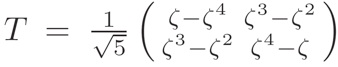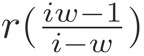PREVIOUS                HOME                NEXT

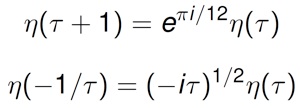
The Dedekind eta function is analytic on the complex upper half plane and satisfies the transformation properties:

The first property follows immediately from the definition of η(τ), while the second property can be derived via an idea of Siegel using Cauchy’s residue theorem. These coupled with the “Key Result” gives the following transformation properties of the function r(τ):

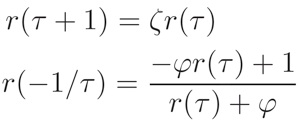
where                    is a primitive fifth root of unity. We can restate the above properties in terms of Möbius transformations: a matrix with complex entries and nonzero determinant acts on the complex  plane plus the point at infinity via

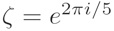
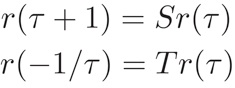
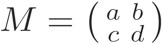
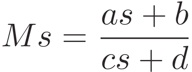
Under this action, we have

where

We found a way to visualize the nontrivial T transformation property by making a change of variable

where w is in the unit disk. To represent a complex valued function on the unit disk, we color each point according to the shade (modulus) and hue (argument) of the corresponding function value

(e.g., zeros are black and a poles are white). We parameterized the matrix T continuously from the identity, and then used SAGE to plot individual frames.

The movie is a visual verification of the T-transformation property since τ mapping to -1/τ is equivalent to w mapping to -w.