My research interest lies in kinetic approaches for multiscale physical systems including applications in seismic wave propagation and inversion, spin-transfer torque in micro-magnetics, and quantum tunneling in quantum chemistry and solid-state physics.
Full Research Statement in PDF(last updated: Oct 5, 2017)
Frozen Gaussian Approximation for 3-D Seismic Tomography
Three-dimensional (3-D) wave-equation-based seismic tomography is computationally challenging in
large scales and high-frequency regime. We present a systematic introduction on applying frozen Gaussian
approximation (FGA) to compute high-frequency sensitivity kernels for adjoint tomography in 3-D earth
models. FGA approximates seismic wavefield by a summation of frozen (fixed-width) Gaussian
wave-packets propagating along ray paths. One can use a relatively small number of Gaussians to get
accurate approximations of high-frequency wavefield. Meanwhile, FGA algorithm can be perfectly
parallelized, which speeds up the computation drastically with a high-performance computing station. In
order to apply FGA to the computation of 3-D high-frequency seismic tomography, first, we reformulate
the FGA so that one can efficiently compute the Green’s functions whose convolutions with source
time function produce wavefields needed for the construction of 3-D kernels; and second, we
incorporate the Snell’s law into the FGA formulation, and asymptotically derive reflection,
transmission and free surface conditions for FGA to compute high-frequency seismic wave
propagation in high contrast media. One paper in presenting these results has been published
in Geophys. J. Int. [11].
The scalar wave equation arising from seismic wave propagation takes the form of
where
where we have used superscripts “ Development of efficient and accurate methods is constantly necessary to improve the
modeling of seismic wave propagation in different situations, especially in complex media with
high contrast heterogeneity. When waves hit the interface where the wave speed The embarrassingly parallel property, less limitation on the time steps in solving the uncoupled
ODEs, and the interface conditions make FGA an efficient method for the large domain and
high-frequency seismic wave simulation. We test the computational efficiency and accuracy of
the FGA in comparison with the spectral element (SPE) method which is widely used in
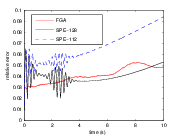
geographic physics. In Figure 1(a), we plot the one-step computational time with respect to
different frequency number Analysis of Semiclassical Limit for Spin-Magnetization Coupling
The spin-magnetization coupling plays a key role in the active control of domain-wall motion and
magnetization reversal in magnetic multilayers, which are the core techniques used in magnetoresistance
random access memories and race-track memories [4]. The Schrödinger-Poisson-Landau-Lifshitz-Gilbert
(SPLLG) system is used to describe a mechanism known as spin-transfer torque that transfers the spin
angular momentum to magnetization dynamics via spin-magnetization coupling, and was introduced in
the seminal works of Slonczweski [18] and Berger [2].
The main goal of this research is to use a quantum-kinetic description and semiclassical analysis to set
up a mathematical theory and foundation of spin polarized transport in ferromagnetic multilayers with
strong orbit coupling from the most fundamental point of view, so that every important detail of
trimming the model can be carefully analyzed. A paper to report these results is going to
appear in Arch. Ration. Mech. Anal., and specifically, we proved the following two theorems
[6]:
Theorem 1 (existence of weak solutions). Consider the SPLLG system where Theorem 2 (semiclassical limit). Under certain assumptions on the initial conditions, there exists a
sequence of solutions ( The coupling of the Schödinger system and the LLG system bring us more difficulties,
which include the non-wellposeness of regular solutions due to the nonlinear LLG system and
the jump discontinuity of the magnetization across the boundary of the domain Then in Semiclassical Models and Methods for Quantum Tunneling
My research works on inter-band tunneling studies the interaction between several coupled potential
energy bands, e.g. , for crystal lattice, the Bloch bands may getting close to each other or even cross, in
which cases particles may transit through the band gap to the other energy band. The study of such
“quantum tunneling” is important in many applications, from quantum dynamics in chemical reaction
[20], semiconductors to Bose-Einstein condensation [3]. In the first approach we considered the quantum
system in phase-space using Wigner transform, and take the off-diagonal terms of the Wigner matrix into
account to capture the tunneling. A paper presenting these results has been published in SIAM Journal on
Multiscale Model. Sim. [8]. In the second approach [9] we studied the Schrödinger equation and
propose a semiclassical-quantum hybrid numerical method. In the following I will take the
Schrödinger equation with a lattice potential as examples and introduce these works in more
detail.
A semiclassical model using Wigner-Bloch theory. We use the Wigner-Bloch theory to derive
semiclassical models for the Schrödinger equation with periodic potentials that account for band-crossing
[7]. Without band-crossing, the classical Vlasov limit can be obtained along each Bloch band [1, 13, 17],
which only includes the diagonal entries of the Wigner-Bloch matrix and valid away from the crossing
zone. In our semiclassical models we include the leading order of the off-diagonal entries, resulting in a
coupled system
Here,
The semiclassical Vlasov system (6) is defined in phase-space and contains a small parameter A Bloch decomposition based hybrid method. In order to reduce the computational complexity, we
develop a new Bloch decomposition-based Gaussian beam (BDGB) method in simulating the periodic
Schödinger equation in the momentum space away from the band-crossings. As an asymptotic solver, the
BDGB method does not have the requirement on the In Figure 3 we show the resulted Bloch coefficients in simulating the Schrödinger equation with a
honeycomb lattice potential using the BDTS and BDGB hybrid method. The Schrödinger
equation with a honeycomb lattice potential can be used to model the electron motion in a
Graphene layer, and due to the existence of the Dirac point, inter-band transitions are very
important in the simulations. But since this problem is defined in two dimensional space,
when
Ongoing and Future Research
Seismic tomography. Seismic tomography is one of the core methodologies for imaging the
structural heterogeneity of the Earth’s interior. Our studies pave the way to directly apply
wave-equation-based seismic tomography methods into real data around their dominant frequencies. We
are currently working on the FGA for elastic wave equations in order to get a more reliable
model in seismic tomography and apply it on real seismic data. On the other hand, though
FGA could improve the efficiency, the adjoint tomography method is still very computational
demanding in CPU time, memory and storage, since it is based on Born approximation and need to
compute the sensitivity kernels. In order to overcome these difficulties, we are working on the
global optimization method using networks and sparse parametrization techniques in order to
make the most of the supper efficiency and parallelizability of FGA in simulating seismic wave
equations.
Spin-magnetization coupling in micro-magnetics. The spin-magnetization coupling in ferromagnetic
materials is definitely a multiscale problem. We have studied this problem in quantum, kinetic and fluid
scalings [6, 5]. However, to study new models which can include more physical details is always
interesting. For example, in our work on the diffusion limit, we didn’t include the self-induced electric
field. We are thinking about to add a self-induced field in order to recover the physical phenomena such as
the linear response. A self-induced field will make the analysis more difficult because then we
don’t have the proper weighted Models and methods in quantum physics. In the semiclassical method for quantum physics, the
main difficulty is that to describe a essential quantum effect such as the tunneling by a semiclassical
model, for which, we have developed non-diagonal systems and hybrid methods [7, 8, 9]. One interesting
phenomena I have being thinking is the Klein paradox in the Graphene layer, for which the Schrödinger
equation with a honeycomb lattice potential and a step potential is considered. The difficulty in
simulating this problem using semiclassical method such as Gaussian beam method is from the
jump discontinuity of the step potential, where quantum tunneling may happen. To over come
this difficulty, an interface condition over the discontinuity is considered to incorporate with
the semiclassical dynamics. One another topic we are working on is the FGA for the 3-D
Dirac equation and consider the semiclassical and non-relativity limits in different regime. The
new nature in FGA brought by the Dirac equation is that we need consider the coupling
dynamics in the two dimensional eigenspace due to the degeneracy of the eigenvalue of the Dirac
Hamiltonian [10], and the Berry connections are included in the coupling. And we are going to
investigate the limiting behavior for both the solution and FGA shall be considered in different
regime.
[1] G. Bal, A. Fannjiang, G. Papanicolaou, and L. Ryzhik. Radiative transport in a periodic
structure. Journal of Statistical Physics, 95(1):479–494, 1999.
[2] L. Berger. Emission of spin waves by a magnetic multilayer traversed by a current. Physical Review
B, 54(13):9353–9358, 1996.
[3] A. Bohm, A. Mostafazadeh, H. Koizumi, Q. Niu, and J. Zwanziger. The Geometric Phase in
Quantum Systems:Foundations, Mathematical Concepts, and Applications in Molecular and Condensed
Matter Physics. Springer, 2012.
[4] A. Brataas, A. Kent, and H. Ohno. Current-induced torques in magnetic materials. Nat. Mater.,
11:372–381, 2012.
[5] L. Chai, C. J. García-Cervera, and X. Yang. Diffusion limit of the Wigner-Landau-Lifshitz-Gilbert
system in ferromagnetic materials. Submitted to Communications in Mathematical Sciences.
[6] L. Chai, C. J. García-Cervera, and X. Yang. Semiclassical limit of the
Schrödinger-Poisson-Landau-Lifshitz-Gilbert system. Archive for Rational Mechanics and Analysis, to
appear.
[7] L. Chai, S. Jin, and Q. Li. Semi-classical models for the Schrödinger equation with periodic
potentials and band crossings. Kinetic and Related Models, 6:505–532, 2013.
[8] L. Chai, S. Jin, Q. Li, and O. Morandi. A multiband semiclassical model for surface hopping
quantum dynamics. Multiscale Modeling & Simulation, 13(1):205–230, 2015.
[9] L. Chai, S. Jin, and P. A. Markowich. A hybrid mthod for computing the Schrödinger equations
with periodic potential with band-crossings in the momentum space. Communications in Computational
Physics, (a special issue in honor of the 80th birthday of Prof. Houde Han), to appear.
[10] L. Chai, E. Lorin, and X. Yang. Frozen Gaussian approximation for 3-D Dirac equations. In
preparation.
[11] L. Chai, P. Tong, and X. Yang. Frozen gaussian approximation for 3-d seismic wave propagation.
Geophysical Journal International, 208(1):59–74, 2017.
[12] L. Chai, P. Tong, and X. Yang. Frozen Gaussian approximation for 3-D seismic tomography.
, submitted.
[13] P. Gérard, P. Markowich, N. Mauser, and F. Poupaud. Homogenization limits and Wigner
transforms. Communications on Pure and Applied Mathematics, 50(4):323–379, 1997.
[14] Z. Huang, S. Jin, P. Markowich, and C. Sparber. A Bloch decomposition-based split-step
pseudospectral method for quantum dynamics with periodic potentials. SIAM Journal on Scientific
Computing, 29(2):515–538, 2008.
[15] Z. Huang, S. Jin, P. A. Markowich, and C. Sparber. Numerical simulation of the nonlinear
Schrödinger equation with multidimensional periodic potentials. Multiscale Modeling & Simulation,
7(2):539–564, 2008.
[16] J. Lu and X. Yang. Convergence of frozen Gaussian approximation for high frequency wave
propagation. Communications on Pure and Applied Mathematics, 65:759–789, 2012.
[17] P. Markowich, N. Mauser, and F. Poupaud. A Wigner-function approach to (semi) classical limits:
Electrons in a periodic potential. Journal of Mathematical Physics, 35:1066–1094, 1994.
[18] J. C. Slonczewski. Current-driven excitation of magnetic multilayers. Journal of Magnetism and
Magnetic Materials, 159(1):L1–L7, 1996.
[19] N. M. Tanushev, B. Engquist, and R. Tsai. Gaussian beam decomposition of high frequency wave
fields. Journal of Computational Physics, 228(23):8856–8871, 2009.
[20] J. Tully and R. Preston. Trajectory surface hopping approach to nonadiabatic molecular collisions:
the reaction of H with D. The Journal of Chemical Physics, 55:562–572, 1971.
[21] S. Zhang, P. Levy, and A. Fert. Mechanisms of spin-polarized current-driven magnetization
switching. Physical review letters, 88(23):236601, 2002.
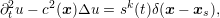
(1) 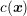 is sound speed,
is sound speed, 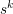 is source time function to model an earthquake event,
is source time function to model an earthquake event,  is the Dirac
delta function, and the wave number
is the Dirac
delta function, and the wave number 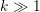 indicates that we are considering seismic wave propagation
of high-frequency (corresponding to short wavelengths). The original FGA formulation is used to
approximate the initial value problem of (1) in the homogeneous case (
indicates that we are considering seismic wave propagation
of high-frequency (corresponding to short wavelengths). The original FGA formulation is used to
approximate the initial value problem of (1) in the homogeneous case (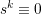 ) by the following
integral,
) by the following
integral,
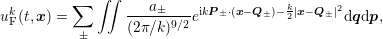
(2) 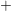 ” and “
” and “ ” to indicate two wave branches respectively, and the
Gaussian center
” to indicate two wave branches respectively, and the
Gaussian center 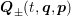 and
and 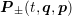 and the amplitude
and the amplitude 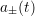 satisfy a system of uncoupled
ODEs [16]. In practice, we should consider an inhomogeneous problem with a non-vanishing source time
function. To achieve this we first get a finite frequency approximation
satisfy a system of uncoupled
ODEs [16]. In practice, we should consider an inhomogeneous problem with a non-vanishing source time
function. To achieve this we first get a finite frequency approximation 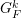 of the Green’s function of (1)
by solving (1) with initial conditions
of the Green’s function of (1)
by solving (1) with initial conditions 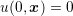 and
and 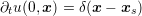 using FGA, and
then we convolve
using FGA, and
then we convolve 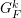 with the source time function
with the source time function 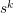 to get the approximation of the
wavefields.
to get the approximation of the
wavefields.
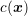 is
discontinuous, proper interface conditions should be incorporated in the FGA formulation to capture
reflected and transmitted waves. To overcome this difficulty we impose the reflection and
transmission condition by applying the Snell’s law and get the leading order terms in asymptotic
expansion
is
discontinuous, proper interface conditions should be incorporated in the FGA formulation to capture
reflected and transmitted waves. To overcome this difficulty we impose the reflection and
transmission condition by applying the Snell’s law and get the leading order terms in asymptotic
expansion  with the reflection coefficient
with the reflection coefficient 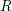 and transmission
coefficient
and transmission
coefficient 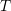 given by
given by 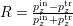 , and
, and 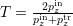 , where we have used
, where we have used  ,
, 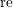 , and
, and
 to indicate the incident, reflected, and transmitted waves respectively, and
to indicate the incident, reflected, and transmitted waves respectively, and 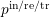 are
velocities determined by Snell’s law. The derivation of the interface condition relays on the
Eulerian formulation of frozen Gaussian approximation [16] and matching of the continuity
conditions.
are
velocities determined by Snell’s law. The derivation of the interface condition relays on the
Eulerian formulation of frozen Gaussian approximation [16] and matching of the continuity
conditions.
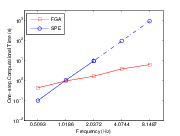
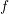 , from which one can observe that the computational time
spent by FGA increases more or less linearly in
, from which one can observe that the computational time
spent by FGA increases more or less linearly in 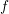 , while that of the SPE increases like
, while that of the SPE increases like
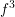 . In Figure 1(b), to achieve a comparable accuracy as FGA, SPE needs 128 elements in
each spatial direction, which requires an average computational three times longer than that
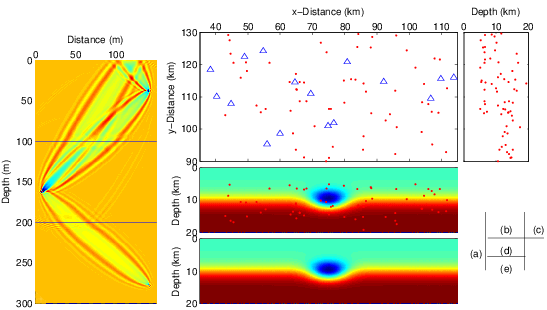
of FGA. We then apply FGA in the computation of the seismic tomography [12]. As shown in Fig.2(a), we apply FGA to the computation of the sensitivity kernels
in 3D seismic inversion in a three-layered cross-well setup. We also apply FGA in the local
earthquake inversion using Landers source-receiver data, where the earthquake events are
marked by red dots and the receivers are marked by blue triangles in Fig.2(b-d). The true
velocity model is shown in Fig.2(d) and a full-waveform inversion result is shown in Fig.2(e).
. In Figure 1(b), to achieve a comparable accuracy as FGA, SPE needs 128 elements in
each spatial direction, which requires an average computational three times longer than that
of FGA. We then apply FGA in the computation of the seismic tomography [12]. As shown in Fig.2(a), we apply FGA to the computation of the sensitivity kernels
in 3D seismic inversion in a three-layered cross-well setup. We also apply FGA in the local
earthquake inversion using Landers source-receiver data, where the earthquake events are
marked by red dots and the receivers are marked by blue triangles in Fig.2(b-d). The true
velocity model is shown in Fig.2(d) and a full-waveform inversion result is shown in Fig.2(e).
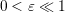 is the renormalized Planck constant in the semiclassical regime,
is the renormalized Planck constant in the semiclassical regime, 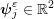 stands
for the
stands
for the 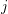 -th spinor,
-th spinor, 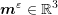 is the magnetization, the potential
is the magnetization, the potential 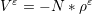 is the Coulomb
interaction, and the effective field
is the Coulomb
interaction, and the effective field ![H ε = Δm ε + H [m ε]+ εs ε,
eff s 2](./RS/RS39x.png) with
with ![H [m ε] = - ∇ (∇N *⋅m ε)
s](./RS/RS40x.png) being the self induced stray field, and
being the self induced stray field, and 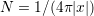 . Then there exists
. Then there exists 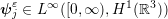 and
and
![ε 1 1
m ∈ C([0,∞ ),H (Ω ))∩ H ([0,T]× Ω )](./RS/RS43x.png) for all
for all 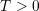 , such that
, such that 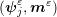 is a weak solution to the
SPLLG system (3).
is a weak solution to the
SPLLG system (3).
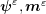 ) of the SPLLG system (3), and
) of the SPLLG system (3), and 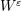 as the Wigner transform of
as the Wigner transform of
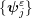 , such that
, such that 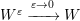 in
in 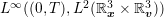 weak*, and
weak*, and 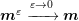 in
in
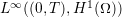 weak*, and
weak*, and  is a weak solution to the following VPLLG system,
is a weak solution to the following VPLLG system,
![∂tW = - v ⋅∇xW + ∇xV ⋅∇vW + i2[ˆσ ⋅m, W ],
∂ m = - m × H + αm × ∂ m,
t eff t](./RS/RS54x.png)
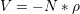 , the density
, the density 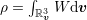 , and the effective magnetic field
, and the effective magnetic field
![He ff = Δm + Hs [m ]](./RS/RS57x.png) .
.
 . The
existence of the global regular solution of the LLG system is still an open problem, and for this
reason we consider the weak solutions in
. The
existence of the global regular solution of the LLG system is still an open problem, and for this
reason we consider the weak solutions in 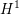 and prove the existence theorem. The jump
discontinuity of the magnetization make the limit of the Wigner equation non-trivial when we
try to estimate the remainder. We apply a mollifier in the intermediate step, successfully
remove the discontinuity and obtain a uniform estimate, and then prove the semiclassical
limit.
and prove the existence theorem. The jump
discontinuity of the magnetization make the limit of the Wigner equation non-trivial when we
try to estimate the remainder. We apply a mollifier in the intermediate step, successfully
remove the discontinuity and obtain a uniform estimate, and then prove the semiclassical
limit.
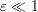 as the rescaled Knudsen number, we considered the s-wave form spin dynamics
coupled with LLG system in the diffusion regime ,
as the rescaled Knudsen number, we considered the s-wave form spin dynamics
coupled with LLG system in the diffusion regime , 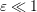 as the rescaled Knudsen number, the BGK collision operator
as the rescaled Knudsen number, the BGK collision operator 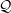 , and the
spin-flip operator
, and the
spin-flip operator 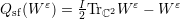 . We studied the existence of solutions in a
weighted
. We studied the existence of solutions in a
weighted  space, and rigorously proved the diffusion limit of the coupled system given by
The first term on the right hand side of (5) represents the precessional motion due to the
sd interaction when the magnetization directions of the spin and the local moments are not
parallel; the second term on the right hand side of (5) represents the spin-flip relaxation, which
recover the diffusion model introduced in by Zhang, Levy and Fert (Nobel Prize, 2007) in
[21]
space, and rigorously proved the diffusion limit of the coupled system given by
The first term on the right hand side of (5) represents the precessional motion due to the
sd interaction when the magnetization directions of the spin and the local moments are not
parallel; the second term on the right hand side of (5) represents the spin-flip relaxation, which
recover the diffusion model introduced in by Zhang, Levy and Fert (Nobel Prize, 2007) in
[21]
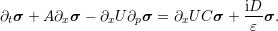
(6) ![T
σ = [σ11,σ12,σ21,σ22]](./RS/RS68x.png) represents the Wigner-Bloch components,
represents the Wigner-Bloch components, 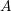 ,
, 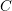 , and
, and 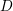 are
are 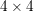 matrices determined by the band structure. In particular, the entries of
matrices determined by the band structure. In particular, the entries of  are the Berry connections,
and
are the Berry connections,
and ![D = diag[0,E2 - E1, E1 - E2,0]](./RS/RS74x.png) with
with 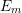 being the
being the  -th Bloch band,
-th Bloch band, 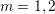 . In this
system different bands are coupled together by
. In this
system different bands are coupled together by 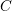 and inter-band transition happens. As
and inter-band transition happens. As  goes to
goes to
 , the off-diagonal entries
, the off-diagonal entries 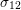 and
and 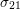 go to
go to  weakly, and the system goes to the classical Vlasov
system
weakly, and the system goes to the classical Vlasov
system
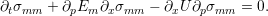
(7)  ,
so numerically solving it requires
,
so numerically solving it requires 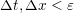 . In order to numerically solve the problem
efficiently, we present a domain decomposition idea based on the asymptotic properties of the
transition coefficients
. In order to numerically solve the problem
efficiently, we present a domain decomposition idea based on the asymptotic properties of the
transition coefficients 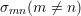 : In a
: In a 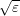 neighborhood of the crossing point, we solve the
semiclassical Vlasov system (6) using a fine mesh with
neighborhood of the crossing point, we solve the
semiclassical Vlasov system (6) using a fine mesh with 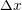 and
and 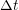 less than
less than 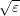 , and out of
the neighborhood we solve the classical Vlasov system (7) using coarse mesh independent of
, and out of
the neighborhood we solve the classical Vlasov system (7) using coarse mesh independent of
 .
.
 -dependent mesh size and time step, and it
reduces the original Schrödinger equation into a system of uncoupled ODEs, thus it can drastically speed
up the computation. Moreover, the BDGB method in momentum space provides us a convenient way to
combine it with the the Bloch decomposition-based time splitting (BDTS) method [14, 15]
in order to capture the inter-band tunneling: Away from the crossing point, the use of the
asymptotic Gaussian beam solution can reduce the computational cost efficiently; around the
crossing point, the direct simulation of the Schrödinger equation by BDTS can capture the
inter-band transitions, and one has to use fine spatial mesh and time steps of
-dependent mesh size and time step, and it
reduces the original Schrödinger equation into a system of uncoupled ODEs, thus it can drastically speed
up the computation. Moreover, the BDGB method in momentum space provides us a convenient way to
combine it with the the Bloch decomposition-based time splitting (BDTS) method [14, 15]
in order to capture the inter-band tunneling: Away from the crossing point, the use of the
asymptotic Gaussian beam solution can reduce the computational cost efficiently; around the
crossing point, the direct simulation of the Schrödinger equation by BDTS can capture the
inter-band transitions, and one has to use fine spatial mesh and time steps of 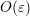 to get
the desired accuracy, but since one can suitably choose the size of computational region as
to get
the desired accuracy, but since one can suitably choose the size of computational region as
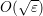 around the crossing point, the numerical cost of this part can also be reduced; and the
exchange of data between different zones is achieved simply by Gaussian beam decomposition
[19].
around the crossing point, the numerical cost of this part can also be reduced; and the
exchange of data between different zones is achieved simply by Gaussian beam decomposition
[19].
 is small, to solve the Schrödinger equation using the BDTS method will be a huge
challenge for the memory and cpu time. With the help of the hybrid method, this example can
be done in one hour on a personal laptop. As it has been shown in Figure 3, the significant
inter-band transition around the Dirac point can be captured clearly using the hybrid method.
is small, to solve the Schrödinger equation using the BDTS method will be a huge
challenge for the memory and cpu time. With the help of the hybrid method, this example can
be done in one hour on a personal laptop. As it has been shown in Figure 3, the significant
inter-band transition around the Dirac point can be captured clearly using the hybrid method.
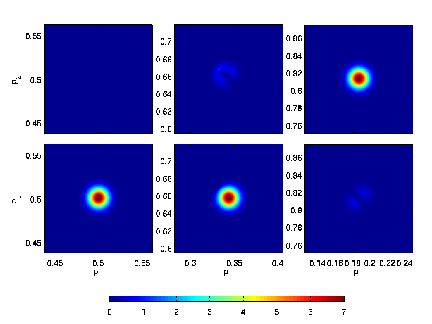
 (left column), the wave
is located at the first band and the second band is empty. At time
(left column), the wave
is located at the first band and the second band is empty. At time 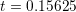 (middle column),
the inter-band transition is happening at the Dirac point. At time
(middle column),
the inter-band transition is happening at the Dirac point. At time 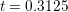 (right column), a
large part of the population is on the upper band.
(right column), a
large part of the population is on the upper band.
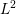 space and the associated conservation law as we did
in [5]. The other model we have been working with is the spin dynamics governed by the
Schrödinger-Maxwell system, and we want to analyze the semiclassical limit and coupling it with
LLG. The main difficulty here is that we don’t have enough regularity of the magnetic field,
so only some weakly coupling regime can be done so far. On the numerical side, to build
efficient numerical solver, investigate the influences of the boundary layers, and construct the
asymptotic preserving scheme for coupling models in different scaling are delicate topics for
me.
space and the associated conservation law as we did
in [5]. The other model we have been working with is the spin dynamics governed by the
Schrödinger-Maxwell system, and we want to analyze the semiclassical limit and coupling it with
LLG. The main difficulty here is that we don’t have enough regularity of the magnetic field,
so only some weakly coupling regime can be done so far. On the numerical side, to build
efficient numerical solver, investigate the influences of the boundary layers, and construct the
asymptotic preserving scheme for coupling models in different scaling are delicate topics for
me.
References
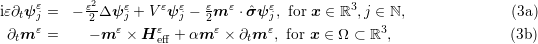
![∂tW ε + 1-(v ⋅∇xW ε(x, v)- ∇x ϕ(x) ⋅∇vW ε(x, v)) = i[ˆσ ⋅m ε,W ε]+-1Q (W ε)+ Qsf(W ε),
ε ε2 (4)
∂tm ε = - γm ε × (Δm ε + Hs [m ε]+ sε)+ m ε × ∂tm ε,](./RS/RS61x.png)
![∂tρ- ∇x ⋅(D ⋅(∇xρ + ∇x ϕρ)) = 0,
∂ts- ∇x ⋅(D ⋅(∇xs + ∇x ϕs)) = - 2m × s - s, (5)
∂ m = - γm × (Δm ε + H [m ε]+ s)+ m × ∂ m.
t s t](./RS/RS66x.png)