Math 134: Dynamical Systems
Instructor: Katy Craig, MS 7354, katy•craig•math at gmail • com
Teaching Assistant: William Oakley, MS 2344, wgoakley at ucla • edu
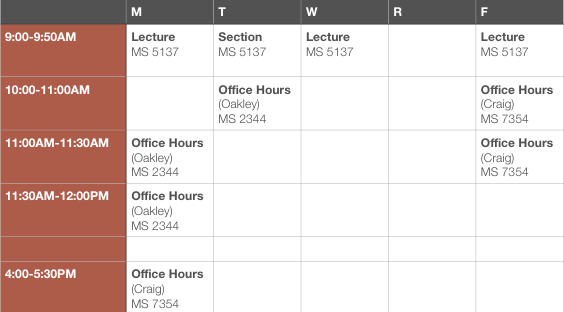
Lecture/Section/Office Hours: Times and Locations
Textbook: S. Strogatz, Nonlinear Dynamics and Chaos, second edition.
Other Recommended References:
S. Strogatz, Lectures on Nonlinear Dynamics and Chaos. (YouTube videos from when our textbook’s author taught a similar course at Cornell)
J. D. Crawford, Introduction to Bifurcation Theory. (Free, if you download from the campus network)
-
S.Wiggins, Introduction to Applied Nonlinear Dynamical Systems and Chaos.
Exams: There will be two midterms and one final exam. The examinations will be closed book and closed note. There will be no retaking or rescheduling of exams under any circumstances, as the grading scheme allows you to drop your lowest midterm score.
First Midterm: Wednesday, February 4th, 9:00-9:50AM
Second Midterm: Wednesday, March 4th, 9:00-9:50AM
Final Exam: Wednesday, March 18th, 8:00-11:00AM
Grading Policy:
Your grade will be calculated based on whichever of the following two schemes results in a higher grade.
Scheme 1: Scheme 2:
Homework: 10% Homework: 10%
First Midterm: 25% Highest Midterm Score: 40%
Second Midterm: 25% Final: 50%
Final: 40%
If you have questions about the grading of any assignment or exam, you have one week after it is handed back to request a regrade.
Prerequisites: Math 33B
Syllabus:
1 Jan 5 (M):
2 Jan 7 (W):
3 Jan 9 (F):
4 Jan 12 (M):
5 Jan 14 (W):
6 Jan 16 (F):
7 Jan 19 (M):
8 Jan 21 (W):
9 Jan 23 (F):
10 Jan 26 (M):
11 Jan 28 (W):
12 Jan 30 (F):
13 Feb 2 (M):
14 Feb 4 (W):
15 Feb 6 (F):
16 Feb 9 (M):
17 Feb 11 (W):
18 Feb 13 (F):
19 Feb 16 (M):
20 Feb 18 (W):
21 Feb 20 (F):
22 Feb 23 (M):
23 Feb 25 (W):
24 Feb 27 (F):
25 Mar 2 (M):
26 Mar 4 (W):
27 Mar 6 (F):
28 Mar 9 (M):
29 Mar 11 (W):
30 Mar 13 (F):
- Mar 18 (W):
Homework:
-
•Homework assignments will be posted on this website and collected Wednesday during lecture.
-
•Only the problems marked with an asterisk should be submitted for grading.
-
•At least one problem on each of the exams will be chosen from the non-asterisked homework problems.
-
•No late homework will be accepted. (Talk to me if you transfer into the course partway through the quarter, and we’ll work something out.)
-
•The lowest two homework grades will be dropped and will not count toward the final grade.
Homework 0 (due Wednesday, January 7th): HW0.pdf
Homework 1 (due Wednesday, January 14th): HW1.pdf (for Q6, the y-axis should be labeled “x(t)” and the x-axis should be labeled “t”)
Homework 2 (due Wednesday, January 21st): HW2.pdf (for Q5, part a, the equation should be "av(t) = A h'(t)" not "av(t) = A · h(t)")
Homework 3 (due Wednesday, January 28th): HW3.pdf (for Q8, you should sketch V(x) as a function of x, not r -- this is a type-o)
Homework 3.5 (extra practice for midterm, not to be turned in): HW3p5.pdf (for Q2, f(x✳︎)<0 should be f’(x✳︎)<0 and -x1/2 should be -|x|1/2)
Your midterm will be of similar difficulty to the homework problems I have assigned, and some problems will be identical to the non-asterisked homework problems.
Homework 4 (due Wednesday, February 11th): HW4.pdf (for Q2, use a computer; for Q3 assume z(0)=0; Q5(b) should read -dV/d\theta = 1)
Homework 5 (due Wednesday, February 18th): HW5.pdf
Homework 6 (due Wednesday, February 25th): HW6.pdf(for Q7, remove the last bit of bullet 2:``but the effect is more severe for the aliens.”)
Homework 6.5 (extra practice for midterm, not to be turned in): HW6p5.pdf (for Q3, it should be \gamma = r \omega^2/g, not r\omega^2 g)
Homework 7 (due Wednesday, March 11th): HW7.pdf (for Q3, the fixed point should be (0,2), not (0,0).)
Homework 7.5 (extra practice for final, not to be turned in): HW7p5.pdf (for Q2, you may assume there are no FPs in the trapping region)
read by today
Strogatz 1.0-1.3
Strogatz 2.0-2.3
Strogatz 2.4-2.6
Strogatz 2.7-2.8
Strogatz 3.0-3.1
Strogatz 3.2-3.3
-
Strogatz 3.4-3.5
-
-
Strogatz 3.6-3.7
Strogatz 4.0-4.3
Strogatz 4.4-4.5
-
Strogatz 5.0-5.1
-
Strogatz 5.2-5.3
Strogatz 6.0-6.2
-
Strogatz 6.3-6.4
Strogatz 6.5-6.6
Strogatz 6.7
Strogatz 6.8
-
Strogatz 7.0-7.1
-
Strogatz 7.2
Strogatz 7.3
Strogatz 8.0-8.1
Strogatz 8.2-8.3
topics to be covered
Dynamical systems and ordinary differential equations
1D flows, linear vs. nonlinear, fixed points, stability, population dynamics
Linear stability analysis, existence and uniqueness, impossibility of oscillations
Potentials, introduction to numerical methods
Intro to bifurcations, saddle-node bifurcation, bifurcation diagrams
Normal forms, transcritical bifurcation
Happy MLK Day!
Pitchfork bifurcation
Pitchfork bifurcation (ctd.), application to overdamped bead on rotating hoop
Application to overdamped bead on rotating hoop (ctd.), dimensional analysis
Imperfect bifurcations, insect outbreak model
Flows on the circle, beating, nonuniform oscillators, ghosts, bottlenecks
Oscillator examples, applications to overdamped pendulum, fireflies
Midterm 1, covering lectures 1-12
2D linear systems, phase portraits
-
Classification of linear systems, characteristic equation, types of fixed points
2D nonlinear systems, existence/uniqueness, trajectories cannot cross
Happy President’s Day!
Stability, fixed points, linearization/effect of nonlinear terms, hyperbolicity, Hartman-Grobman theorem
Special nonlinear systems, conservative/reversible systems, heteroclinic/homoclinic orbits
Application of nonlinear phase plane analysis to classic pendulum problem
Index theory, local vs global methods
Index theory continued
Limit cycles
Midterm 2, covering lectures 13-24
Ruling out limit cycles, gradient systems, Liapunov functions
Existence of closed orbits, Poincare-Bendixson thm, trapping regions, impossibility of chaos
Bifurcations in higher dimensions, saddle-node, transcritical, pitchfork bifurcations
Hopf bifurcation, supercritical/subcritical/degenerate types
Final Exam, 8-11AM, covering lectures 1-30
Outline of Course:
Part 1: One dimensional flows
-
•fixed points and linear stability analysis
-
•bifurcation theory
-
-saddle-node, transcritical, pitchfork
-
•flows on the circle
Part 2: Two dimensional flows
-
•linear vs. nonlinear systems
-
•phase plane analysis
-
•limit cycles
-
•bifurcation theory
-
-saddle-node, transcritical, pitchfork, Hopf