Talks: Videos and Slides
For latest talks and videos see: youtube:atzberger.
- Deep Learning Approaches for Non-linear Dynamics: Generative Approaches for Data-Driven Simulations, MiC Seminar, DOE ORNL [Video]
- Generative Machine Learning Approaches for Data-Driven Modeling of Dynamics, DDPS Seminar, DOE LLNL [Video]
- Protein Drift-Diffusion in Curved Membranes: Surface Fluctuating Hydrodynamics Methods, APS March Meeting Talk (biophysics session),[Video]
- Surface Fluctuating Hydrodynamics Methods: Soft Materials with Fluid-Structure Interactions within Curved Fluid Interfaces, World Congress in Computational Mechanics (WCCM) Talk, [PDF] [GoogleSlides] [Video]
- Stochastic Immersed Boundary Methods for Fluid-Structure Interactions, New York University (NYU), [PDF] [Video]
- Learning Nonlinear Dynamics of Physical Systems: Geometric Dynamic Variational Autoencoders (GD-VAEs), [Video]
- SELM: Software Tutorial: Fluid-Structure Interaction Simulations, LAMMPS Workshop, [Video]
- Regression, Kernel Methods, Regularization, LASSO, Tomography Example, Machine Learning Lecture, [PDF] [MicrosoftSlides] [Video (Part 1)] [Video (Part 2)]
- MLMOD: Machine Learning Methods for Data-Driven Modeling in LAMMPS (Overview), LAMMPS Workshop, [Video]
- Statistical Learning Theory, Generalization Errors, and Sampling Complexity Bounds, Machine Learning Lecture, [PDF] [MicrosoftSlides]
- Complexity Measures, Radamacher, VC-Dimension, Machine Learning Lecture, [PDF] [MicrosoftSlides]
- Support Vector Machines, Kernels, Optimization Theory Basics, Machine Learning Lecture, [PDF] [MicrosoftSlides]
- Unsupervised Learning, Dimension Reduction, Manifold Learning, Machine Learning Lecture, [PDF] [MicrosoftSlides]
- Neural Networks and Deep Learning Basics, Machine Learning Lecture, [PDF] [GoogleSlides]
- Convolutional Neural Networks (CNNs) Basics, Machine Learning Lecture, [PDF] [GoogleSlides]
- Recurrent Neural Networks (RNNs) Basics, Machine Learning Lecture, [PDF] [MicrosoftSlides]
- Generative Adversarial Networks (GANs), Machine Learning Lecture, [PDF] [MicrosoftSlides]
- Learning Nonlinear Dynamics of Physical Systems: Variational Autoencoders (VAEs), ML-DL Workshop, Sandia National Laboratories, July 2021, [Video]
- GRIT Talk (public lecture aimed at general audiences, see video below), [PDF] [Video]
- UCLA IPAM Talk at Workshop on Partial Order: Mathematics, Simulations and Applications, [PDF] [GoogleSlides][Video]
- Fluctuating Hydrodynamics Approaches for Mesoscopic Modeling and Simulation (Part 1), Stanford University: Summer School on Multiscale Modeling of Materials Workshop, [PDF] [GoogleSlides] [Video]
- Fluctuating Hydrodynamics Approaches for Mesoscopic Modeling and Simulation (Part 2), Stanford University: Summer School on Multiscale Modeling of Materials Workshop, [PDF] [GoogleSlides] [Video]
Videos
For latest talks and videos see
Atzberger YouTube Channel
Surface Fluctuating Hydrodynamics Methods: Soft Materials with Fluid-Structure Interactions within Curved Fluid Interfaces, WCCM Conference Talk, Biomechanics and Mechanobiology Session, Nov 2020.
[link to video] [PDF] [GoogleSlides]
The Hidden Role of Mathematics and Computation in Scientific Discovery and Engineering
UCSB Seminar Series: Groundbreaking Research / Innovative Technology (GRIT), July 2016.
Public lecture aimed at general audiences.
Fluctuating Hydrodynamics Approaches for Lipid Bilayer Membranes
UCLA IPAM Talk at Workshop on Partial Order: Mathematics, Simulations and Applications, January 2016.
[link to video] [slides PDF] [link to UCLA IPAM Workshop] [software]
Fluctuating Hydrodynamics Approaches for Mesoscopic Modeling and Simulation (Part 1)
Stanford University: Summer School on Multiscale Modeling of Materials Workshop, June 2016.
[link to video] [slides PDF] [software]
Fluctuating Hydrodynamics Approaches for Mesoscopic Modeling and Simulation (Part 2)
Stanford University: Summer School on Multiscale Modeling of Materials Workshop, June 2016.
Tutorial for Mango-Selm Package: How to Setup the Models and Simulations using Jupyter Notebooks and Python.
Interactive Session
Fluid-Structure Interaction Modeling and Simulation
Lecture: Regression, Kernel Methods, Regularization, LASSO, Tomography Example: [PDF] [MicrosoftSlides]
[link to video (part 1)] [link to video (part 2)]
Additional videos are available on the Atzberger YouTube Channel and gallery page.
For more information on my current research please see the publications section or the main homepage.
Course Notes and Supplemental Materials
Data Science and Machine Learning
Slides: Statistical Learning Theory, Generalization Errors, and Sampling Complexity Bounds:
[MicrosoftSlides] [PDF]
Slides: Complexity Measures, Radamacher, VC-Dimension:
[MicrosoftSlides] [PDF]
Slides: Support Vector Machines, Kernels, Optimization Theory Basics:
[MicrosoftSlides] [PDF]
Slides: Regression, Kernel Methods, Regularization, LASSO, Tomography Example:
[MicrosoftSlides] [PDF] [Video (Part 1)] [Video (Part 2)]
Slides: Unsupervised Learning, Dimension Reduction, Manifold Learning:
[MicrosoftSlides] [PDF]
Slides: Neural Networks and Deep Learning Basics:
[GoogleSlides] [PDF]
Slides: Convolutional Neural Networks (CNNs) Basics:
[GoogleSlides]
[PDF]
Slides: Recurrent Neural Networks (RNNs) Basics:
[MicrosoftSlides]
[PDF]
Slides: Generative Adversarial Networks (GANs):
[MicrosoftSlides]
[PDF]
Image Classification using Convolutional Neural Networks (course exercise)
Facial Recognition and Feature Extraction (course exercise)

- [Jupyter Notebook PDF]
- [Jupyter Notebook Code]
- [data-folder]
- [Kaggle: Facial Recognition (SVM)]
- [Kaggle PDF]
Machine Learning Course Link

Machine Learning: Foundations and Applications Course (MATH CS 120) [course-link]
Machine Learning: Foundations and Applications Course (MATH 260J) [course-link]
Finite Element Methods: Slides
- Introduction to FEM and Ritz-Galerkin Approximation [PDF] Δ [GoogleSlides]
- Sobolev Spaces [PDF] [GoogleSlides]
- Finite Element Spaces [PDF] [GoogleSlides]
- Finite Element Approximation Properties and Convergence [PDF] [GoogleSlides]
- Variational Formulation of Elliptic PDEs [PDF] [GoogleSlides]
- Elasticity Theory [PDF] [GoogleSlides]
- Finite Element Mixed Methods [PDF] [GoogleSlides]
Non-linear Optimization: Notes
Monte-Carlo Methods
Mathematical Finance
- An Introduction to Portfolio Theory [PDF]
- The Black-Scholes-Merton Approach to Pricing Options [PDF]
- Contingent Claims and the Arbitrage Theorem [PDF]
- A Brief Introduction to Stochastic Volatility Modeling [PDF]
| Partial Differential Equations: Course Notes: | ||
| (please submit any typos here) | ||
| - Method of Characteristics, Solving First-Order PDEs | [PDF] | |
| - Classifying Second-Order PDEs and Canonical Forms | [PDF] | |
| - Wave Equation and Solution Techniques | [PDF] | |
| - Diffusion Equation and Solution Techniques | [PDF] | |
| - Separation of Variables | [PDF] | |
| - Fourier Methods | [PDF] | |
| - Elliptic PDEs and Fourier Approaches | [PDF] | |
| - Discrete Fourier Transforms (DFTs) and Approximate Solutions of PDEs | [PDF] | |
| - Finite Difference Methods and von Neumann Analysis | [PDF] | |
Dynamical Systems and ODEs
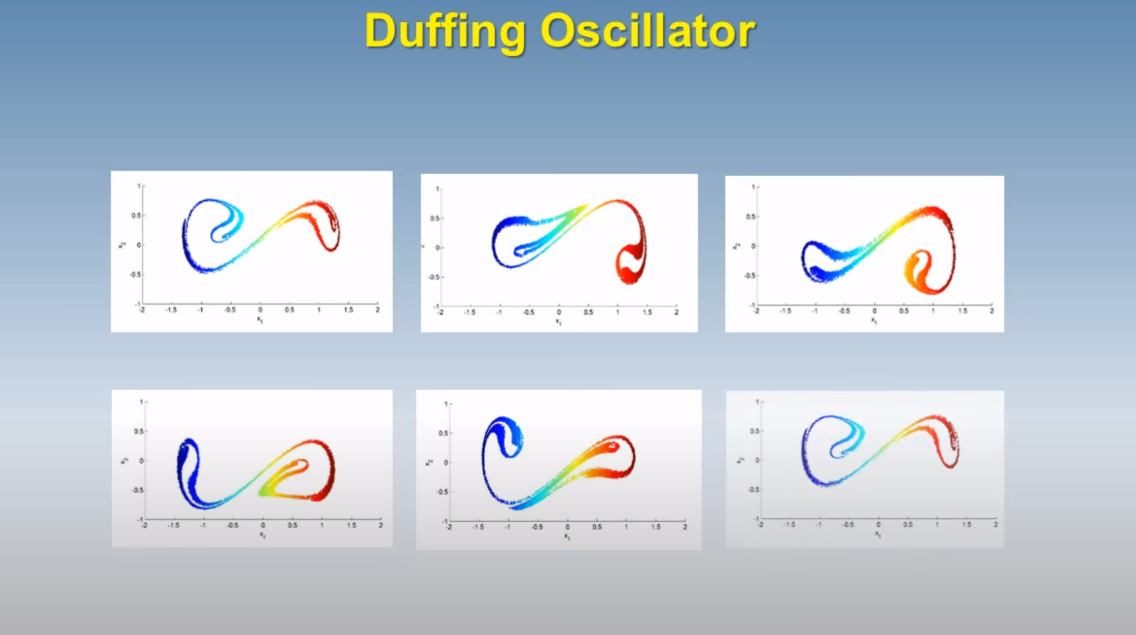
- Poincare Sections of the Duffing Oscillator: [link to video]
The specific parameters are
delta=0.25, gamma=0.3, omega=1.0.
For more information on my current research please see the publications section or the main homepage. Additional videos are also available on the Atzberger YouTube Channel.