Course Notes and Supplemental Materials
Data Science and Machine Learning
Slides: Statistical Learning Theory, Generalization Errors, and Sampling Complexity Bounds:
[MicrosoftSlides] [PDF]
Slides: Complexity Measures, Radamacher, VC-Dimension:
[MicrosoftSlides] [PDF]
Slides: Support Vector Machines, Kernels, Optimization Theory Basics:
[MicrosoftSlides] [PDF]
Slides: Regression, Kernel Methods, Regularization, LASSO, Tomography Example:
[MicrosoftSlides] [PDF] [Video (Part 1)] [Video (Part 2)]
Slides: Unsupervised Learning, Dimension Reduction, Manifold Learning:
[MicrosoftSlides] [PDF]
Slides: Neural Networks and Deep Learning Basics:
[GoogleSlides] [PDF]
Slides: Convolutional Neural Networks (CNNs) Basics:
[GoogleSlides]
[PDF]
Slides: Recurrent Neural Networks (RNNs) Basics:
[MicrosoftSlides]
[PDF]
Slides: Generative Adversarial Networks (GANs):
[MicrosoftSlides]
[PDF]
Image Classification using Convolutional Neural Networks (course exercise)
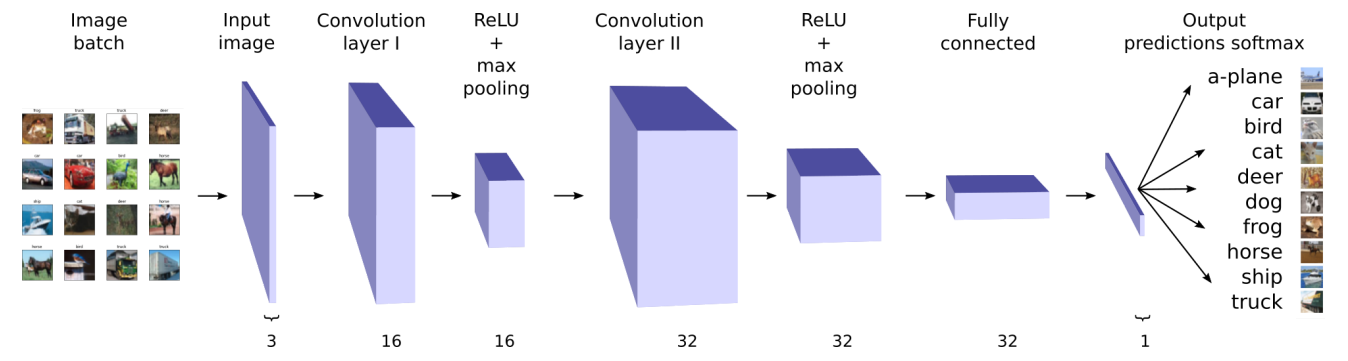
Jupyter Notebook Codes | CIFAR10 PDF | MNIST PDF | Data Folder
Facial Recognition and Feature Extraction (course exercise)
Jupyter Notebook Codes | Jupyter PDF | Data Folder | Kaggle: Facial Recognition (SVM) | Kaggle PDF
Machine Learning Exercise 1: [PDF]
Kaggle1: Linear Regression (warm-up) [Python Code]
Machine Learning Exercise 2: [PDF]
Kaggle2: [Kaggle PDF]
Digit Classification MNIST (k-NN)
Machine Learning Exercise 3: [PDF]
Kaggle3: [Kaggle PDF] Facial Recognition (SVM)
Facial Recognition Codes: [Jupyter Notebook PDF]
[Jupyter Notebook Code]
[data-folder]
Machine Learning Exercise 4: [PDF]
Machine Learning Exercise 5: [PDF]
Kaggle4: [Kaggle PDF] Image Classification: Convolutional Neural Networks (CNNs)
Neural Network Codes: [Jupyter Notebook CIFAR10 PDF] [Jupyter Notebook MNIST PDF]
[Jupyter Notebook Codes] [data-folder]
Machine Learning Take-home Final [PDF]
Machine Learning Course Link
Machine Learning: Foundations and Applications Course (MATH CS 120) [course-link]
Machine Learning: Foundations and Applications Course (MATH 260J) [course-link]
Finite Element Methods: Slides
- Introduction to FEM and Ritz-Galerkin Approximation [PDF] [GoogleSlides]
- Sobolev Spaces [PDF] [GoogleSlides]
- Finite Element Spaces [PDF] [GoogleSlides]
- Finite Element Approximation Properties and Convergence [PDF] [GoogleSlides]
- Variational Formulation of Elliptic PDEs [PDF] [GoogleSlides]
- Elasticity Theory [PDF] [GoogleSlides]
- Finite Element Mixed Methods [PDF] [GoogleSlides]
- Elasticity Theory: Numerical Example [PDF] [GoogleSlides]
Partial Differential Equations (PDEs)
| Supplemental Course Notes: | |||
| (please submit any typos here) | |||
| - Method of Characteristics, Solving First-Order PDEs | [PDF] | ||
| - Classifying Second-Order PDEs and Canonical Forms | [PDF] | ||
| - Wave Equation and Solution Techniques | [PDF] | ||
| - Diffusion Equation and Solution Techniques | [PDF] | ||
| - Separation of Variables | [PDF] | ||
| - Fourier Methods, Solving Parabolic, and Hyperbolic PDEs | [PDF] | ||
| - Elliptic PDEs and Fourier Approaches | [PDF] | ||
| - Discrete Fourier Transforms (DFTs) and Approximate Solutions of PDEs | [PDF] | ||
| - Finite Difference Methods and von Neumann Analysis | [PDF] | ||
| Codes: Numerical Examples | |||
| - Wave Equation | [jupyter notebook] [PDF] | ||
| - Diffusion Equation | [jupyter notebook] [PDF] | ||
| - Fourier Series Examples | [jupyter notebook] [PDF] | ||
| - Discrete Fourier Transform (DFT) | [jupyter notebook] [PDF] | ||
Non-linear Optimization: Notes
Monte-Carlo Methods
Mathematical Finance
- An Introduction to Portfolio Theory [PDF]
- The Black-Scholes-Merton Approach to Pricing Options [PDF]
- Contingent Claims and the Arbitrage Theorem [PDF]
- A Brief Introduction to Stochastic Volatility Modeling [PDF]
Dynamical Systems and ODEs
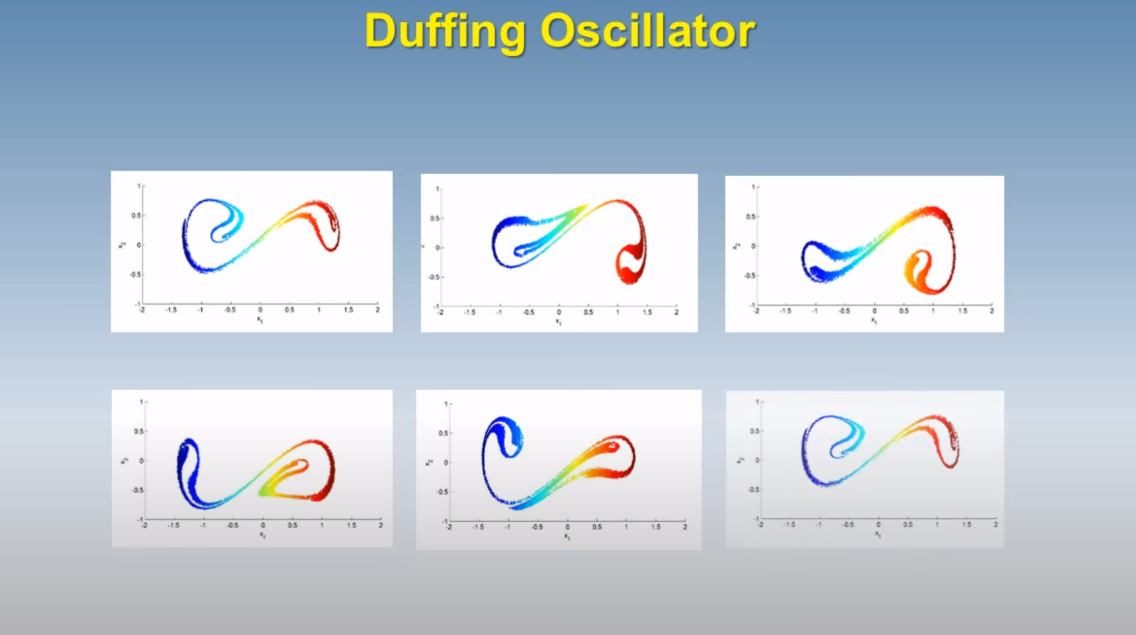
- Poincare Sections of the Duffing Oscillator: [link to video].
The specific parameters are
delta=0.25, gamma=0.3, omega=1.0.